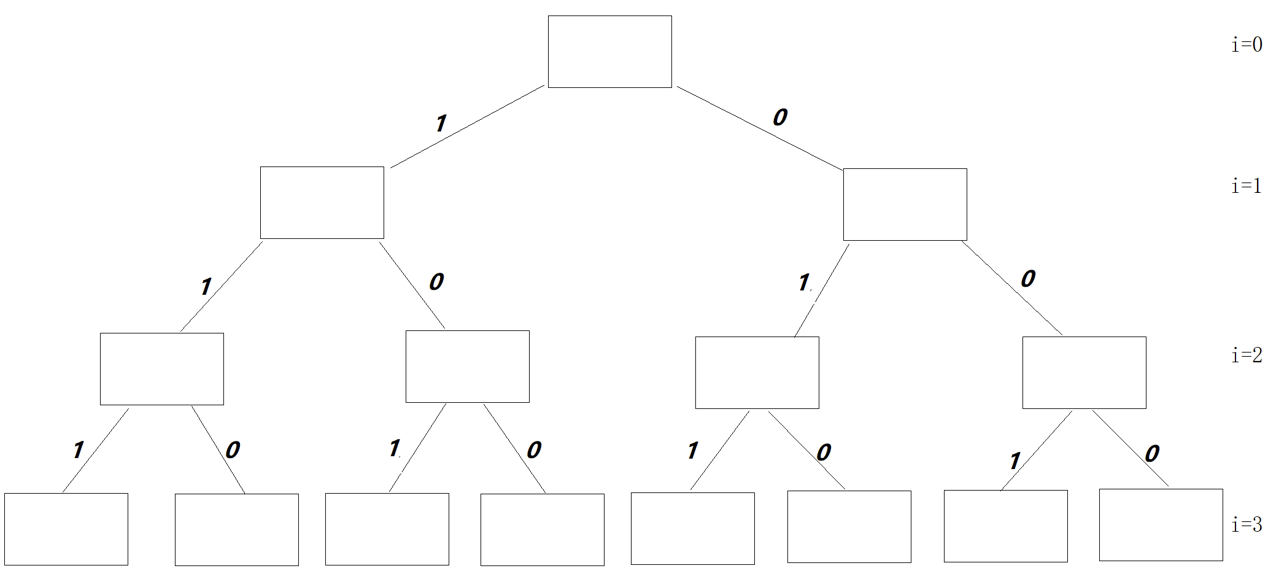
子集树
排列树
子集树可以用来解决从集合中挑选一些元素以达到一定条件的问题。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 void func (int arr[], int length, int x[]) if (i == length) { for (int j = 0 ; j < length; ++j) { if (x[j] == 1 ) { std::cout << arr[j] << " " ; } } std::cout << std::endl; } else { x[i] = 1 ; func (arr, i + 1 , length, x); x[i] = 0 ; func (arr, i + 1 , length, x); } }
另一种形式:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 void func (int arr[], int i, int length, int x[]) if (i == length) { for (int j = 0 ; j < length; ++j) { if (x[j] == 1 ) { std::cout << arr[j] << " " ; } } std::cout << std::endl; } else { for (int k = 1 ; k >= 0 ; --k) { x[i] = k; func (arr, i + 1 , length, x); } } }
但是这一种形式不太利于直接添加剪支操作。
剪左支的条件:选择第i数时,当前累计和已经超过了given_sum,则没必要再往下进行。i数时,剩下的i + 1到n的累计和(即剩余未处理的数的和,注意,不是”未选择“,而是”未处理“,”处理“是层级别的概念,”选择“是左右子树概念)rest加上当前累计和不够given_sum,则没必要往下进行。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 #include <iostream> #include <vector> int arr[] = { 4 ,8 ,12 ,16 ,7 ,9 ,3 };int given_sum = 18 ;int res = 0 ;std::vector<int > aux; bool func (int * arr, int i, int length) bool have = false ; if (i == length) { if (res == given_sum) { for (int v : aux) { std::cout << v << " " ; } std::cout << std::endl; have = true ; } } else { if (res + arr[i] <= given_sum) { res += arr[i]; aux.push_back (arr[i]); return func (arr, i + 1 , length); res -= arr[i]; aux.pop_back (); } int rest = 0 ; for (int j = i + 1 ; j < length; ++j) { rest += arr[j]; } if (res + rest >= given_sum) { return func (arr, i + 1 , length); } } return have; } int main () bool have = func (arr, 0 , sizeof (arr) / sizeof (arr[0 ])); if (!have) { std::cout << "have not resolution." << std::endl; } }
更好的写法:在main函数中先给出rest的总值。在处理第i + 1层前,减去第i个数。处理完第i + 1层后,即开始回溯到i,则i层又活了,需要加回第i个数。i + 1到n)的和,而替换成每次只需简单地减、加一个arr[i]。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 #include <iostream> #include <vector> int arr[] = { 4 ,8 ,12 ,16 ,7 ,9 ,3 };int given_sum = 18 ;int res = 0 ;int rest = 0 ;std::vector<int > aux; bool func (int * arr, int i, int length) bool have = false ; if (i == length) { if (res == given_sum) { for (int v : aux) { std::cout << v << " " ; } std::cout << std::endl; have = true ; } } else { rest -= arr[i]; if (res + arr[i] <= given_sum) { res += arr[i]; aux.push_back (arr[i]); return func (arr, i + 1 , length); res -= arr[i]; aux.pop_back (); } if (res + rest >= given_sum) { return func (arr, i + 1 , length); } rest += arr[i]; } return have; } int main () for (int v : arr) { rest += v; } bool have = func (arr, 0 , sizeof (arr) / sizeof (arr[0 ])); if (!have) { std::cout << "have not resolution." << std::endl; } }
同时还需要注意,未处理和未选择的概念不要混淆,我第一次写成了如下形式:这是错误的。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 else { if (res + arr[i] <= given_sum) { res += arr[i]; rest -= arr[i]; aux.push_back (arr[i]); return func (arr, i + 1 , length); res -= arr[i]; rest += arr[i]; aux.pop_back (); } if (res + rest >= given_sum) { return func (arr, i + 1 , length); } } return have; } int main () for (int v : arr) { rest += v; } }
这与上面的含义完全不一样。我们要做的是”处理“、”未处理“时,rest变量的变化。而不是”选择“、”未选择“时,rest变量的变化。”处理“是层级别的概念,”选择“是左右子树概念。arr[i];不管选不选,走不走左右子树,之后rest都要加上arr[i]。
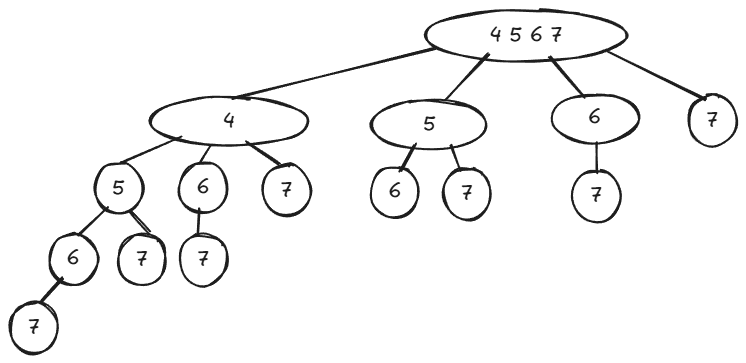
以下程序生成的是如下图的子集树:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 #include <iostream> #include <vector> int arr[] = { 4 ,8 ,12 ,16 ,7 ,9 ,3 };int given_sum = 18 ;int res = 0 ;int rest = 0 ;std::vector<int > aux; void func (int i, int length, int number) if (number == 0 ) { for (int v : aux) { std::cout << v << " " ; } std::cout << std::endl; } else { for (int k = i; k < length; ++k) { if (number >= arr[k]) { aux.push_back (arr[k]); func (k + 1 , length, number - arr[k]); aux.pop_back (); } } } } int main () func (0 , 7 , given_sum); return 0 ; }
输出:8 7 3
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 else { for (int k = i; k < length; ++k) { if (number >= arr[k]) { aux.push_back (arr[k]); func (k, length, number - arr[k]); aux.pop_back (); } } } } int main () func (0 , 7 , given_sum); return 0 ; }
输出
1 2 3 4 5 6 7 8 9 4 4 4 3 3 4 4 7 3 4 8 3 3 4 7 7 8 7 3 12 3 3 9 9 9 3 3 3 3 3 3 3 3 3
序列有不同的排列方式,求解原始序列的某一种特定的排列方式以达到一定条件的问题。
排列问题可以表示为以下形式:R = { r 1 , r 2 , r 3 , ⋯ , r n } R=\{ r_1, r_2, r_3, \cdots, r_n \} R = { r 1 , r 2 , r 3 , ⋯ , r n } n n n R i = R − { r i } R_i=R-\{r_i\} R i = R − { r i } X X X p e r m ( X ) perm(X) p e r m ( X ) ( r i ) p e r m ( X ) (r_i)perm(X) ( r i ) p e r m ( X ) p e r m ( X ) perm(X) p e r m ( X ) r i r_i r i R R R
当n = 1 n=1 n = 1 p e r m ( R ) = ( r ) perm(R)=(r) p e r m ( R ) = ( r ) r r r R R R
当n > 1 n>1 n > 1 p e r m ( R ) perm(R) p e r m ( R ) ( r 1 ) p e r m ( R 1 ) , ( r 2 ) p e r m ( R 2 ) , ⋯ , ( r n ) p e r m ( R n ) (r_1)perm(R_1),(r_2)perm(R_2),\cdots,(r_n)perm(R_n) ( r 1 ) p e r m ( R 1 ) , ( r 2 ) p e r m ( R 2 ) , ⋯ , ( r n ) p e r m ( R n ) R i = R − { r i } R_i=R-\{r_i\} R i = R − { r i }
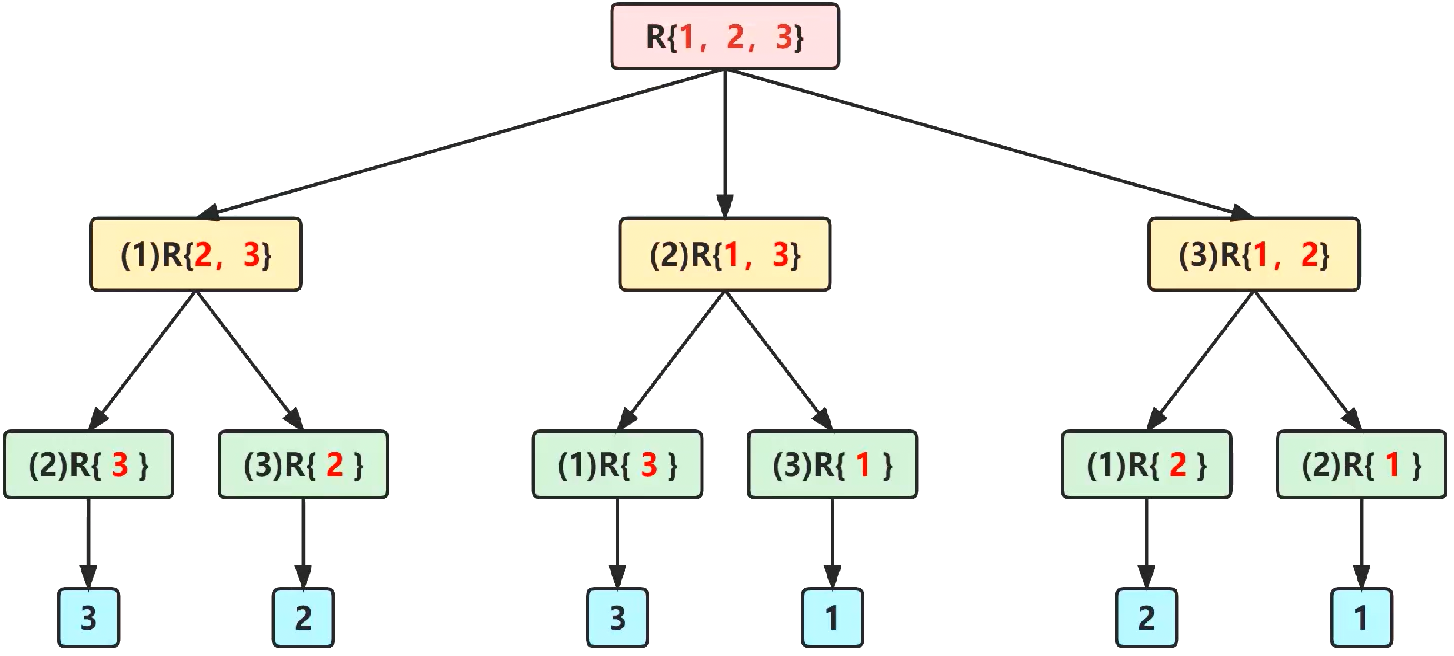
比如:R = { 1 , 2 , 3 } R=\{1,2,3\} R = { 1 , 2 , 3 } p e r m ( R ) perm(R) p e r m ( R ) ( 1 ) p e r m ( { 2 , 3 } ) , ( 2 ) p e r m ( { 1 , 3 } ) , ( 3 ) p e r m ( { 1 , 2 } ) (1)perm(\{2,3\}),(2)perm(\{1,3\}),(3)perm(\{1,2\}) ( 1 ) p e r m ( { 2 , 3 } ) , ( 2 ) p e r m ( { 1 , 3 } ) , ( 3 ) p e r m ( { 1 , 2 } )
在第i层视角上,集合内每个元素都依次与第i个位置进行交换。如下图:元素1到了第1的位置,则出现:(1)R{2,3},元素2到了第1的位置,则出现:(2)R{1,3},元素3到了第1的位置,则出现:(3)R{1,2}。
于是,在代码中,我们可以写出for循环的条件:第i层时,(以下表述均对应实际元素数组的下标,例如:第0层,对应第1个元素的位置,下标为0),就要把从k(用k作为i的副本)到n-1的元素循环与第i个位置进行交换。
交换后再次进行perm计算,下一次的i更新为i+1。
从层次视角看,本层的perm调用结束后,不要忘记把状态回退,即第k个元素换回i位置。
当到达第n层,达到递归终止条件,这时arr数组中记录的各个元素的位置即为此时序列的某种全排列。直接全部输出即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 #include <iostream> void swap (int * arr, int i, int j) int tmp = arr[i]; arr[i] = arr[j]; arr[j] = tmp; } void func (int * arr, int i, int length) if (i == length) { for (int j = 0 ; j < length; ++j) { std::cout << arr[j] << " " ; } std::cout << std::endl; } else { for (int k = i; k < length; ++k) { swap (arr, i, k); func (arr, i + 1 , length); swap (arr, i, k); } } } int main () int arr[] = { 1 , 2 , 3 , 4 }; const int length = sizeof (arr) / sizeof (arr[0 ]); func (arr, 0 , length); }
输出
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 1 2 3 4 1 2 4 3 1 3 2 4 1 3 4 2 1 4 3 2 1 4 2 3 2 1 3 4 2 1 4 3 2 3 1 4 2 3 4 1 2 4 3 1 2 4 1 3 3 2 1 4 3 2 4 1 3 1 2 4 3 1 4 2 3 4 1 2 3 4 2 1 4 2 3 1 4 2 1 3 4 3 2 1 4 3 1 2 4 1 3 2 4 1 2 3
在n × n n\times n n × n n n n
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 void NiceBackTrack () x[1 ] = 0 ; int k = 1 ; while (k >= 1 ) { x[k] += 1 ; while ((x[k]) <= n) && !Place (k)) { x[k] += 1 ; } if (x[k] <= n) { if (k == n) { sum += 1 ; PrintQ (); } else { k += 1 ; x[k] = 0 ; } } else { --k; } } }