C语言_数据类型_浮点型

发表于2021-08-18更新于2025-07-30阅读次数

课件

image-20210818232054410

image-20210818232259910
image-20210818232907404

image-20210818231225754

image-20210818231301755
image-20210818231320838
image-20210818231341094
image-20210818231554889
image-20210818231457059

image-20210818231917144

二进制

二进制怎么转换为十进制？0101 -> 5

1
2
3
4
5
次数：  3  2  1  0
权值：  0  1  0  1
  0 + 1 * 2^2 + 0 + 1 * 2^0
= 0 +   4     + 0 +    1
= 5

十进制怎么转换为二进制？5 -> 101

1
2
3
4
5
6
7
2  | 5                     
   ---------               _
  2  | 2   ......     1   /|\    后3位
     ---------             |
    2  | 1   .....    0    |     后2位
        -------            |
          0   ......  1    |     后1位

负数怎么表示

以下均是在4位机下讨论

负5？

5 + x = 0 -> 0101 + x = 0 -> 0101 + 1010 = 1111, 1111 + 1 = 0, x = 1010 + 1 = 1011

负数用补码表示，是原码的反码加1。

负8？

先求8的原码的反码，再加1：8: 1000 -> 0111 + 1 -> 1000

负8的补码居然是它自己？

搞了半天发现，我们一开始就说明了，在4位机下讨论，那么有符号数的范围只有-8 ~ 7，根本就不存在8一说。所以，无法求得8的原码，也因此无法求8的补码。（为什么1000不能代表8的原码？因为有符号数中第一位代表符号位！）

16进制

1
2
3
 0101 1100
  5    C
=> 0x5C

数字字面常量的规则：只要第一位是数字，那么代表这是个数字。而0开头的数字，不带x的是8进制（0___），带x的是16进制（0x___），带b的是2进制（0b___）。

16进制的格式化输出的描述符为%x，代表unsigned hexadecimal integer，是无符号十六进制整型。

1
2
3
4
5
6
int main()
{
    unsigned char ucVal = 0x5cu;//0x5c是数字，u是无符号指示
    printf("%hhu\n", ucVal);    //92
    printf("%hhx\n", ucVal);    //5c
}

8进制

8进制的格式化输出的描述符为%o，代表unsigned octal，是无符号8进制数。

1
2
3
 01 011 100
  1   3   4
=> 0134
1
2
3
4
5
6
int main()
{
    unsigned char ucVal = 0134u;//0134是数字，u是无符号指示
    printf("%hhu\n", ucVal);    //92
    printf("%hho\n", ucVal);    //134
}

2进制

输出2进制：需要把C语言设置为17标准。

2进制没有格式化输出的描述符。

1
2
      0101 1100
=> 0b 0101 1100
1
2
3
4
5
6
int main()
{
    unsigned char ucVal = 0b0101'1100u; // '为分割符号，便于人性化输入，可有可无
    printf("%hhu\n", ucVal);    //92
    printf("%hho\n", ucVal);    //134
}

integer

32 bits, 4 Bytes

  1. 区分有符号、无符号，其中有符号的signed可以省略；无符号带int的整型的int可以省略，其他无符号整型不能省；long int中的int可以省略
  2. 字面常量（8、8u）也是有类型的，不带后缀默认是有符号数，带u是无符号数。

long int

ISO标准中提到，long int的大小不得小于int。目前微软long int的大小为32bits、4字节；而在Linux下为64bits、8字节。

long指示类型的长度，涉及到长度，格式化输出时，需要注意加上length specifiers，即长度描述符。

long long int

64bits、8字节

short int

16bits、2字节

针对于整型字面常量的长度描述符没有专门用于short的，因为C语言字面常量最小为32位。如果比32位小的，一律向下兼容。归根结底是因为数据总线最少一次传32位。

但是，针对于printf中的格式化输出，还是要区分长度的，对应short的长度描述符为h。

char

如果要打印十进制整数，那么对应char的长度描述符为hh。格式描述符为i或u。

而如果要打印字符，那么对应的格式描述符为c。

ASCII码：形式上是字符图形，但本质上是整数，如'a'是97。

整型类测试

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
int main()
{
    /* integer: 32bits */
    /*signed*/ int iVal = 8;
    unsigned /*int*/ uVal = 8u;
    printf("%i\n", iVal);
    printf("%u\n", uVal);
    /* long int: 32bits */
    /*signed*/ long /*int*/ lVal = 9l;
    unsigned long /*int*/ ulVal = 9ul;
    printf("%li\n", lVal);
    printf("%lu\n", ulVal);
    /* long long int: 64bits */
    /*signed*/ long long /*int*/ llVal = 9ll;
    unsigned long long /*int*/ ullVal = 9ull;
    printf("%lli\n", llVal);
    printf("%llu\n", ullVal);
    /* short int: 16bits */
    /*signed*/ short /*int*/ sVal = 9; //9后面没有专门用于short的长度指示符
    /*unsigned*/ short /*int*/ usVal = 9u;
    printf("%hi\n", sVal);             //但是格式化输出有，要加上h
    printf("%hu\n", usVal);
    /* char: 8bits */
    /*signed*/ char cVal = 9;
    unsigned char ucVal = 9u;
    printf("%hhi\n", cVal);
    printf("%hhu\n", ucVal);
    unsigned char ucVal2 = 'a';
    printf("%c\n", ucVal2);
}

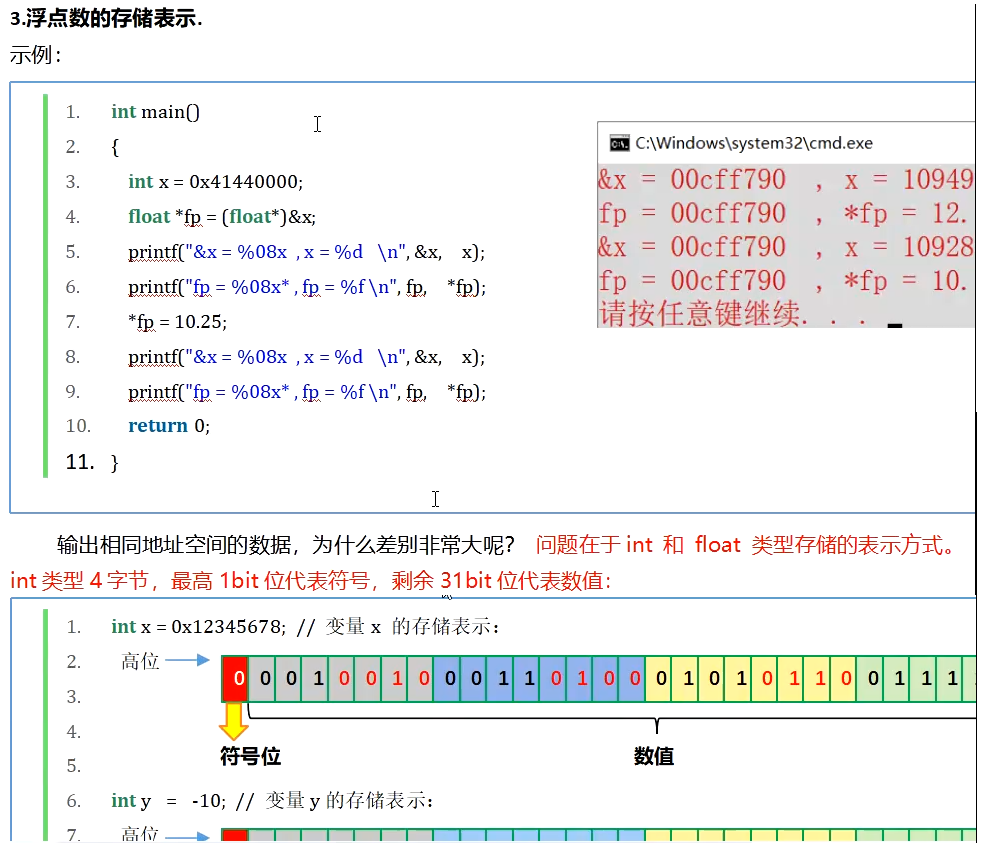
浮点型

计算机中整型和浮点型的计算是在不同的处理器下完成的。整型处理器是由x86部分完成的，浮点型处理器是由x87部分完成的。因为整型和浮点型的格式是不一样的。

小数默认都是有符号数。

1010.1101二进制小数化为十进制小数。依然按照每一位的权重展开计算：

\begin{align} & 1\times2^3+0\times2^2+1\times2^1+0\times2^0+1\times2^{-1}+1\times2^{-2}+0\times2^{-3}+1\times2^{-4}\\ & =8+2+\frac{1}{2}+\frac{1}{4}+\frac{1}{16}\\ & =10.8125 \end{align}

10.8125十进制小数如何化为二进制小数？整数部分是一直进行余2运算，而小数部分如何化？即0.1101。

\begin{align} 0.8125\times2&=1.625\cdots1\\ 0.625\times2&=1.250\cdots1\\ 0.25\times2&=0.500\cdots0\\ 0.5\times2&=1.000\cdots1\\ &end \end{align}

与求整数的二进制不同，求余之后，整数二进制的结果从下往上顺位。而小数二进制是从上往下顺位。

0.13化为二进制小数时会遇到无限循环的现象：

\begin{align} 0.13\times2&=0.26\cdots0\\ 0.26\times2&=0.52\cdots0\\ 0.52\times2&=1.04\cdots1\\ 0.04\times2&=0.08\cdots0 -- cycle\\ 0.08\times2&=0.16\cdots0\\ 0.16\times2&=0.32\cdots0\\ 0.32\times2&=0.64\cdots0\\ 0.64\times2&=1.28\cdots1\\ 0.28\times2&=0.56\cdots0\\ 0.56\times2&=1.02\cdots1\\ 0.02\times2&=0.04\cdots0\\ 0.04\times2&=0.08\cdots0 -- cycle\\ &\cdots \end{align}

float（单精度）

全称：single point float，单精度浮点数。32 bits, 4 Bytes

格式描述符用f。代表十进制浮点数（Decimal floating point）

1
2
3
4
5
int main()
{
    float fVal = 5.0f;   //加f后缀指示其为float类型字面常量
    printf("%f\n", fVal);
}

double（双精度）

全称：double point float，双精度浮点数。64 bits, 8 Bytes

格式描述符也是用f。代表十进制浮点数（Decimal floating point）

1
2
3
4
5
int main()
{
    double dVal = 5.0;  //字面小数常量不加后缀，默认为double类型
    printf("%f\n", dVal);
}

long double

Modern Cpp和新的C标准才有的。标准指出long double长度不得小于double。在微软编译器下等于double长度，有些编译器是大于double长度的。为什么微软如此保守呢？因为CPU的字长一般还是64位。如果大小设计超过64位的话，就需要两个时钟周期来完成数据的传输。

需要注意，long double的格式描述符依旧为f，%后面的长度描述符不再是l而是大写的L。而字面常量的后缀还是小写的l。

1
2
3
4
5
int main()
{
    long double ldVal = 5.0l; // 加l后缀
    printf("%Lf\n", ldVal);   // 加L前缀，格式描述符
}

科学计数法

651.32怎么表示（字面常量）？

  1. 651.32
  2. 6.52132e+2，其中+可以省略

科学计数法的格式描述符为e或E。表示：Scientific notation (mantissa/exponent), lowercase/uppercase

0.065132呢？6.5132e-2

1
2
3
4
5
6
7
int main()
{
    double dVal = 6.52132e+2;
    printf("%f\n", dVal); // 652.132000
    printf("%e\n", dVal); // 6.521320e+02
    printf("%E\n", dVal); // 6.521320E+02
}

float内存结构（IEEE754标准）

IEEE754标准。所有处理器，无论手机上的ARM架构还是服务器处理器都是遵循这个标准。

三部分：sign（符号位）、exponent（指数）、mantissa（底数）

sign（符号位）

sign（符号位） - 1 bit - 1代表负，0代表正

exponent（指数）

首先，指数是一个有符号数。
负数，是补码表达的。八位二进制来说，0000 0000表示0，则 1111 1111表示-1，1000 0000表示-128，0111 1111表示127，这是有符号正数的最大值，再加1就溢出了。本来的范围是：-128 ~ 127
但是，浮点数中指数位置存储的是偏移值，如果是float，存储的值是加了127的。因此，指数为1时，应该存储1 + 127 = 128，存储1000 0000；指数为2时，应该存储2 + 127 = 129，存储1000 0001。因此，加127后，范围就变成了：-1 ~ 254。
而指数全0、全1，在浮点数中有特殊含义。所以，范围就变成了：1 ~ 254。减去127之后，实际的范围就变成了：-126 ~ 127。

举一个例子：7.25怎么表示？先转化为二进制：0111.01，带权的形式则是：1.1101 * 2^2，即右移2位，指数为2。
实际存储的二进制形式：

1
2
0     1000 0001            (1)110 1000 0000 0000 0000 0000`
符   指数位（2+127=129）    底数位（23位）前面有个隐藏的1，不在这23位中

exponent（指数） - 8 bits - 标准里规定：

在exp位模式（the bit pattern of exp）既不全为0，也不全为1时，浮点数值为规格化的值。
阶码字段在这种情况下，被解释为以偏置（biased）形式表示的有符号整数（原文：the exponent field is interpreted as representing a signed integer in biased form）。
那么，阶码字段的值为：E=e−BiasE = e - Bias。
其中ee是无符号数，即直接通过exp位模式计算得出。
BiasBias是一个固定值2k−1−1,k=exp的位数,单精度下是8位,双精度下是11位2^{k-1}-1, k = exp的位数, 单精度下是8位, 双精度下是11位。比如，float，指数二进制位数为8位时，Bias就是128-1=127。
单精度下Bias=27−1=127Bias=2^7-1=127。
因此EE范围：(1−127)∼(254−127)=−126∼127(1-127)\sim(254-127)=-126\sim127，表示在2进制下可以右移127位、左移126位。
e和最终的移位值之间的对应关系：1 = -126、2 = -125，…，253 = 126、254 = 127。

由此，看出，不能简单地把exp位模式看做有符号数直接计算得到移位数值，如果直接当做有符号数计算的话，范围变成了：1000'0000 ~ 0111'1111 = -128 ~ 127。和标准规定的对应不上！

为什么要预留出来exp位模式全0或全1的情况？

  1. 全0是为了能让浮点数可以表示0或者表示非常接近于0.0的数。此情况在标准中称为：“非规格化的值”。这种情况下，阶码值（移位值）规定为E=1−BiasE=1-Bias。并且要特别注意：底数的值是位模式直接计算出来的，也就是小数字段的值，不包含隐含的开头的1。即：0.XXXX，不再是1.XXXX！

使阶码值为1−Bias1-Bias而不是简单的−Bias-Bias​似乎是违反直觉的。但是这种方式提供了一种从非规格化值平滑转换到规格化值的方法。

  1. 非规格化数有两个用途。首先，它们提供了一种表示数值0的方法，因为使用规格化数，我们必须总是使M≥1M\geq1，因此就不能表示0。实际上，+0.0+0.0的浮点表示的位模式为全0：符号位是0，阶码字段全为0（表明是一个非规格化值），而小数域也全为0，这就得到M=f=0M=f=0。令人奇怪的是，当符号位为1，而其他域全为0时，我们得到值−0.0-0.0。根据IEE的浮点格式，值+0.0+0.0和−0.0-0.0在某些方面被认为是不同的，而在其他方面是相同的。
  2. 非规格化数的另外一个功能是表示那些非常接近于0.00.0的数。这提供了一种属性，称为逐渐溢出（gradual underflow），其中，可能的数值分布均匀地接近于0.00.0。而刚才提到的使阶码值为1−Bias1-Bias而不是简单的−Bias-Bias，就是为这个做铺垫的！详看CSAPP-3rd P80。
  3. 全1是为了能让浮点数表示
    1. 无穷大 - 底数全0时
    2. NaN - 底数非0时

mantissa（底数）

  1. mantissa（底数） - 23 bits - 范围、精度：lg⁡224≈7.2247\lg 2^{24} \approx 7.2247，即可以表示7位十进制数。
    1. 因为要用科学计数法，底数第一位必须是1，因此可以省略第一位。因此此处的23位可以表达24位二进制数。

7.25的IEEE754表示：

0 1000'0001 110'1000'0000'0000'0000'0000

浮点数的好处

  1. 虽然精度小，但是可表示的范围大（指数的作用）。
  2. 能表达实数（除了小数，也能表示整数、0）
  3. 能表达NaN（Not A Number），0除以0的结果就是NaN。
    1. 0 1111'1111 100'0000'0000'0000'0000'0000
  4. 能表达正负inf（无穷大），比如1除以0。
    1. 正无穷：0 1111'1111 000'0000'0000'0000'0000'0000
    2. 负无穷：1 1111'1111 000'0000'0000'0000'0000'0000

怎么比较浮点数

首先是不带等号的大小判断（<、>）

  • 对于 a < b、a > b 这种​​大小关系比较​​，通常可以​​安全地直接使用运算符​​。
  • 因为即使存在微小的舍入误差，只要这个误差不足以改变大小关系的本质（即误差远小于 a 和 b 本身的差值），结果就是正确的。
  • 判断 a 是否严格大于 b 时，应该使用 a > b，而不是 !(a <= b)（后者涉及相等判断，不精确）。

特殊值的比较

  • 特殊值如 NaN (Not a Number) 与任何值（包括自己）比较，== 都返回 false，!= 都返回 true。必须用专门的函数检查：
    • Python: math.isnan(x)
    • C/C++: isnan(x) (来自 math.h 或 cmath)
    • Java: Double.isNaN(x) / Float.isNaN(x)
  • 检查无穷大：
    • Python: math.isinf(x)
    • C/C++: isinf(x)
    • Java: Double.isInfinite(x) / Float.isInfinite(x)

涉及到两个浮点数是否相等时

绝对不能直接用 == 或 != 来判断两个浮点数是否“相等”！​​
因为浮点数在计算机内部使用 IEEE 754 标准以二进制存储小数，很多十进制小数无法精确表示（例如 0.1），计算过程中也会积累微小的舍入误差。
正确的比较方法是​​允许一定的误差范围（容差 epsilon）​​：

  1. ​​检查近似相等 (Approximate Equality)：​​
    • 计算两个浮点数 a 和 b 的绝对差值：diff = abs(a - b)
    • 定义一个非常小的正数作为容忍度 epsilon（例如 1e-9, 1e-12, 具体值取决于你的精度要求）。
    • 如果 diff <= epsilon，则认为 a 和 b 在 epsilon 的误差范围内是“相等”的。
    • 但是这个容差是绝对容差，有缺陷，见下：
  • 检查相对相等 (Relative Equality - 更稳健)：​​
    • 当数值大小差异巨大时，固定绝对容差可能不合适（比如比较 1e9 和 1e9+1e-9 时差值很小，但比较 1e-9 和 2e-9 时用绝对容差 1e-9 会认为相等）。相对容差考虑数值的大小。
    • rel_tol: 相对容差（如 1e-5, 1e-9）
    • abs_tol: 绝对容差下限（保证接近零的数也能比较，例如设为 1e-12）

下面主要论述，为什么需要相对相等（使用相对容差）

直接使用绝对相等的容差（比如 abs(a - b) <= 1e-9）在大多数情况下是有效的。但是，它有一个显著的缺点：当比较的数值本身非常大或者非常小（靠近零）时，这个固定大小的绝对容差就显得不合理了。

  1. ​​问题场景一：数值巨大​​

    • 例子：比较 a = 1, 000, 000, 000 (1e9) 和 b = 1, 000, 000, 001 (1e9 + 1)
    • 它们的绝对差是 |a - b| = 1。
    • 如果你设定的绝对容差 epsilon = 1e-9（即 0.000000001），那么 1 > 1e-9，程序会判断它们​​不相等​​。
    • 但直觉上，10亿和10亿零1之间的_相对误差_非常小（大约是 1 / 1e9 = 1e-9）。在很多科学计算或工程领域，这个精度已经足够了，我们可能希望认为它们_相对相等_。
    • ​​结论：​​ 当数值本身很大时，一个固定的小绝对容差过于严格，忽略了数值的量级。

  2. ​​问题场景二：数值极小（接近零）​​

    • 例子：比较 a = 0.000001 (1e-6) 和 b = 0.000002 (2e-6)
    • 它们的绝对差是 |a - b| = 0.000001 (1e-6)。
    • 如果你设定的绝对容差 epsilon = 1e-9（即 0.000000001），那么 1e-6 > 1e-9，程序会判断它们​​不相等​​。
    • 但是，它们的相对差非常大（一个是另一个的两倍，相对误差高达 1e-6 / 1e-6 = 1 或 100%）。实际上，它们_不应_被看作是近似相等的。
    • ​​结论：​​ 当数值本身很小时，一个固定的小绝对容差又过于宽松，可能把差别很大的两个数判断为相等。
    • ​​更麻烦的问题：比较接近零的数​​
      • 例子：比较 a = 0.000000001 (1e-9) 和 b = 0.000000002 (2e-9)
      • 绝对差 |a - b| = 1e-9，如果我们设定的绝对容差也是 1e-9，那么程序会认为它们相等。
      • 例子：比较 a = 1e-20 和 b = 2e-20
      • 绝对差 |a - b| = 1e-20。一个合理的绝对容差（比如 1e-9）远远大于这个差值（1e-9 > 1e-20），所以程序也会认为它们相等。但从相对角度看，b 是 a 的两倍！
      • ​​总结：​​ 对于非常接近零的数，即使设置了一个看似很小的绝对容差，也可能过于宽松，无法反映数值之间的真实相对误差。这时甚至需要一个更小的、不切实际的绝对容差才能区分它们，而相对相等可以自然地处理这种情况（此时相对误差会很大）。

​​相对相等的解决方案：引入相对容差​​

相对相等的核心思想是：​​判断两个数是否近似相等的标准，应该与它们自身的_大小_有关。​​

  1. ​​核心公式：​​

    abs(a - b) <= max(rel_tol * max(|a|, |b|), abs_tol)

    • rel_tol: ​​相对容差（relative tolerance）​​。这是一个很小的正数，表示你能接受的_最大相对误差_（例如 0.01 表示 1% 的相对误差，1e-5 表示 0.001% 的相对误差，1e-9 表示极小的相对误差）。这个值需要根据你的具体应用场景（你对精度的要求）来设定。
    • abs_tol: ​​绝对容差下限（absolute tolerance）​​。这也是一个很小的正数（例如 1e-12）。它的作用是确保当 a 和 b 都_非常非常接近零_时，公式仍然有效。

  2. ​​公式解读：​​

    • max(|a|, |b|): 取 a 和 b 的绝对值中较大的那个。这代表了参与比较的两个数在数值上的大致_量级（Scale）_。
    • rel_tol * max(|a|, |b|): ​​动态计算的相对容差​​。这个容差会根据 a 和 b 的当前量级自动调整：
      • 当 a 和 b 很大时，这个值会变大，可以容忍较大的绝对差值（只要相对误差小）。
      • 当 a 和 b 很小时（但还没有小到必须依赖 abs_tol），这个值会变小，要求更小的绝对差值才能被视为相等。
    • max( ..., abs_tol): 取 动态计算的相对容差 和 abs_tol 中​​较大的那个​​作为最终的容差阈值。
      • 当 a 和 b 远离零时，动态计算的相对容差 通常会远大于 abs_tol，所以max 的结果就是相对容差。
      • 当 a 和 b 非常接近零（或者其中一个为零）时，动态计算的相对容差 (rel_tol * max(|a|, |b|)) 会变得非常小（接近于零）。如果此时没有 abs_tol，即使两个非常接近零但彼此不同的数（比如 1e-20 和 2e-20，差值 1e-20），也会因为 1e-20 > 某个几乎为零的动态相对容差 (比如 1e-9 * 2e-20 = 2e-29) 而被错误地认为_不相等_（而实际上根据相对误差，它们差异很大）。更极端的是比较 0 和一个很小的数（比如 1e-30），动态计算的相对容差 会变成 0，没有 abs_tol 就无法进行有效比较。加入 abs_tol 提供了这个绝对下限。
      • abs_tol 就是为了确保在这种情况下，公式不会因为 动态计算的相对容差 太小而失效。它会提供一个最低限度的绝对容差保证（比如 1e-12）。如果 |a - b| <= abs_tol，即使 a 和 b 本身很小（导致 rel_tol * max(|a|, |b|) 更小），也能认为它们在绝对意义上足够接近零。

  3. ​​举例说明：​​

    • ​​情况一：大数值（相对容差主导）​​
      • a = 1e9, b = 1e9 + 1000 (|a-b|=1000)
      • 设 rel_tol=1e-6, abs_tol=1e-9
      • max(|a|,|b|) ≈ 1e9
      • 动态相对容差 = 1e-6 * 1e9 = 1000
      • max(1000, 1e-9) = 1000
      • 1000 (|a-b|) <= 1000 (阈值) → ​​相对相等（成立）​​
    • ​​情况二：中等数值（相对容差主导）​​
      • a = 3.141592, b = 3.141593 (|a-b|=0.000001)
      • 设 rel_tol=1e-6, abs_tol=1e-9
      • max(|a|,|b|) ≈ 3.1416
      • 动态相对容差 ≈ 1e-6 * 3.1416 ≈ 3.1416e-6
      • max(3.1416e-6, 1e-9) ≈ 3.1416e-6
      • 0.000001 (1e-6) ≈ 1e-6 < 3.1416e-6 (阈值) → ​​相对相等（成立）​​
      • 注意：如果只用 abs_tol=1e-9，1e-6 > 1e-9，会被判为不相等。相对容差（≈ 3e-6）更合理。
    • ​​情况三：小数值（绝对容差主导）​​
      • a = 1e-10, b = 2e-10 (|a-b|=1e-10)
      • 设 rel_tol=1e-6, abs_tol=1e-12
      • max(|a|,|b|) = 2e-10
      • 动态相对容差 = 1e-6 * 2e-10 = 2e-16 (非常小！)
      • max(2e-16, 1e-12) = 1e-12 (因为 1e-12 远大于 2e-16)
      • 1e-10 (|a-b|) <= 1e-12? ​​1e-10 > 1e-12​​ → ​​不相等（成立）​​
        • 解释： 虽然它们很小（都在 1e-10 量级），但b是a的2倍！相对误差极大。绝对容差 1e-12 无法容忍 1e-10 这么大的差，所以正确判定不相等。动态相对容差 2e-16 在这里太小而没起作用，abs_tol 1e-12 提供了合适的判断依据。
    • ​​情况四：非常接近零（绝对容差主导）​​
      • a = 0, b = 1.5e-12
      • 设 rel_tol=1e-6, abs_tol=1e-12
      • max(|a|,|b|) = 1.5e-12
      • 动态相对容差 = 1e-6 * 1.5e-12 = 1.5e-18 (极其小！)
      • max(1.5e-18, 1e-12) = 1e-12
      • 1.5e-12 (|a-b|) <= 1e-12? ​​1.5e-12 > 1e-12​​ → ​​不相等（成立）​​
      • 想让它被判定为接近零（相等）：
        • 可以设置更大的 abs_tol，比如 abs_tol=1.6e-12
        • 1.5e-12 <= 1.6e-12 → ​​相对相等（成立）​​
    • ​​情况五：相对容差和绝对容差都参与（通常发生在中等或较小数值）​​
      • 公式选取两者中较大的作为最终容差，确保在两种标准中满足其一即可视为相等。

在代码中使用：​​

在 Python 中，推荐使用标准库 math.isclose：

1
2
3
4
import math

if math.isclose(a, b, rel_tol=1e-9, abs_tol=1e-12):
    print("a and b are considered close")
  • rel_tol：相对容差，通常 1e-9 是一个较高的精度要求，1e-6 或 1e-3 可能用于精度要求较低的领域。根据你的需求设定。
  • abs_tol：绝对容差下限，通常设置为一个非常小的数（如 0.0， 1e-12, 1e-15），或者当你知道要处理接近零的数时，设置成一个合适的、比“显著差异”要小的值（例如，如果你的数据精度极限是 1e-10，abs_tol=1e-12 可能就太小了，需要设成 1e-9 或更大，但这时最好通过相对容差来覆盖非零区域）。 abs_tol 最主要的作用是确保 a 和 b 都接近零时比较逻辑仍然工作。

​​总结：​​

相对相等 (abs(a - b) <= max(rel_tol * max(|a|, |b|), abs_tol)) 是一种更​​稳健（Robust）​​的浮点数近似相等判断方法。它通过结合​​相对容差​​（rel_tol）来解决大数值比较的问题，以及​​绝对容差下限​​（abs_tol）来解决非常接近零的数值比较的问题，从而在各种不同的数值量级上提供更合理、更一致的比较结果。在复杂应用中，优先考虑使用相对相等而不是简单的绝对容差相等。

练习题

CSAPP-3rd P93 2.84

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
填写下列程序的返回值，这个程序测试它的第一个参数是否小于或者等于第二个参数。假定函数f2u返回一个无符号32位数字，其位表示与它的浮点参数相同。你可以假设两个参数都不是NaN。两种0，+0和一0被认为是相等的。
int float_1e(float x, float y){
unsigned ux=f2u(x);
unsigned uy=f2u(y);
/*Get the sign bits*/
unsigned sx=ux >>31;
unsigned sy=uy >>31;
/*Give an expression using only ux，uy，sx，and sy*/
return;
}
如果使用判断就比较简单，下面是不使用判断.
第一个参数是否小于等于第二个参数，将可能满足的情况（即会返回1的情况）进行分类处理。
情况一：两个参数相等且为0， 根据IEEE规则，0用Denormalized表示，且有+0(0x0)和-0(0x80000000)两种表示 所以通过左移一位来比较
==>ux << 1 == 0 && uy << 1 == 0
情况二：第一个参数为负(此时ux>>31为sx=0x1得到!sx=0) ，第二个参数为0或者正数(此时uy>>31为sy=0x0 !sy=1)
==>(sx && !sy)
反之，若第一个参数为正或者0， 第二个参数为负，这种情况肯定返回0，就不需要特殊处理。
情况三：两个参数都为正
==>(!sx && !sy && ux <= uy)
情况四：两个参数都为负，此时根据IEEE的定义 正数可以用无符号整数的升序进行排列（正数越大 无符号数越大） 负数可以用无符号整数的升序进行排列（负数越小，无符号数越大）
==>(sx && sy && ux >= uy)
四种情况或运算,满足一种就返回1。

讨论题

下列哪些浮点数是符合标准的？1.e0、1.2e0、.2e0、123、1e0、2e4.2、1.2、.e5
​​2e4.2：不符合​。指数部分 (e4.2) 包含了小数点 .。指数必须是一个​​整数​​（可正可负，如 4, -2, +10）。
.e5：​​不符合​。尾数部分 .e5 缺少有效的数字。前面只有小数点 . 而没有跟随任何数字。必须在小数点前后至少有一方包含数字（如 .1, 1., 1.2, 1e5）。

两道诡异的题目

1
2
3
4
5
6
7
8
int main()
{
    char a = 100;
    char b = 200;
    char c = a + b;
    printf("%d %d\n", c, a+b);
}
//输出结果为44 44

a和b同为8位有符号整型类数据。直接加和，a+b等于300。a和b都是char型，最后得出的结果也是char型：因为溢出了8位的最大范围（0~255），所以需要模256，最终300转换后的结果等效于44。

44是存储在内存中的数据，最终显示给人类的还是44，因为44没有超过127，也就不用涉及到补码来表示负数。（反之的情况，如果模后的结果是128，则表示人类所看到的负数-128；如果模后的结果是255，则表示-1）

既然a和b都是char型，最后得出的结果也是char型，所以"c"和"a+b"两者代表的意义是一样的，最终都是char型下的44。于是输出结果为44。

上面的题目只是乐呵一下，下面的题目才诡异莫测，如果对计算机的底层运算法则、流程不详，那么是无法领会的。

1
2
3
4
5
6
7
8
int main()
{
    unsigned char a = 100;
    unsigned char b = 200;
    char c = a + b;
    printf("%d %d\n", c, a+b);
}
//输出结果为44 300

我们默认我们在x86体系架构下的、字长为32位的环境下运行。根据微机原理x86的描述，我们的通用寄存器有eax/ebx/ecx/edx。其中低16位叫做ax/bx/cx/dx。再分，低16位中的高8位叫做ah/bh/ch/dh、低8位叫做al/bl/cl/dl。

经过测试，在VS2019编译器下，反汇编代码得出：a+b这个语句的运算首先要把a和b的值分别存放到寄存器eax/ecx中。注意：eax和ecx都是32位寄存器，如果把a和b的值分别存放到寄存器eax/ecx中，意味着存放了原来的8位有效数据外，前面的24位都需要补位，而无符号整型数据补前位时用0补位。
存数据之后，对两数的加操作是：add eax,ecx。即加操作是在寄存器内累加的。那么即使300超过了255，本应溢出的数据仍然能有效保存在寄存器eax中（即关键的第9位——“1”）。

接下来：

对于char c = a + b;，对c的赋值是通过eax赋值的，因为声明了c是有符号char型，赋值时存在隐形类型转换，即要进行隐式的切片操作，将切除前24位，留下后8位。所以：这里编译器只把低八位即AL赋给了c。因此，上述的eax寄存器中关键的第9位——"1"失效了，只保留了后八位，最终打印c的结果是44。

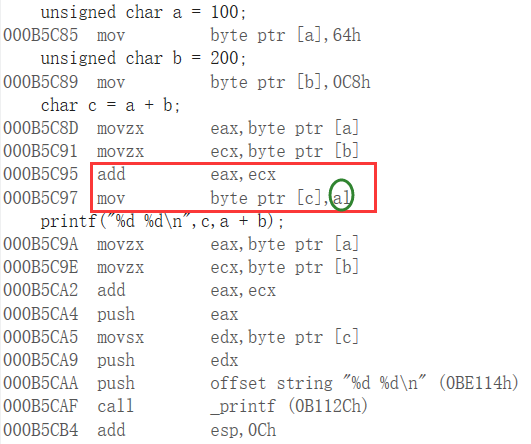
image-20210818214251517

对于a + b;，a和b在eax寄存器中直接加和的结果是300，即使超过了255，本应溢出的数据仍然能有效保存在寄存器eax中（即关键的第9位——“1”）。而我们格式化控制的输出是%d，即我们要拿4个字节即32位有符号整型来识别内存的数据，并在最后转为十进制数，所以打印出来是300。（其实如果拿%u来打印更合适，即32位无符号整型来识别内存的数据，并在最后转为十进制数，最后打印出来也是300）

习题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
int main()
{
    char c = 128;
    unsigned char uc = 128;
    unsigned short us = 0;
    us = c + uc;
    printf("%x \n",us);//0
    
    us = (unsigned char)c+uc;
    printf("%x \n",us);//16:100->10:256
    
    us = c+(char)uc;
    printf("%x \n",us);//2:1111 1111 1000 0000+1111 1111 1000 0000=>(1) 1111 1111 0000 0000 -> 16:ff00
    
    //同us = c + uc;原理一样，都是相当于把c存放到16位ax寄存器中，自然需要补位，而c原本是有符号数，则补符号位"1"。
	//强转为(unsigned short)就表示存放到16位ax寄存器中。其实我们不用人为地显式写出"(unsigned short)"，因为c+uc肯定需要达到统一类型，自然要把char c隐式转为unsigned short，即无符号16位数据。
    us = (unsigned short)c+uc;
    printf("%x \n",us);//1111 1111 1000 0000+0000 0000 1000 0000=>(1) 0000 0000 0000 0000 =>0 -> 16:0
    
    return 0;
}//0 100 ff00 0

image-20210818224646093

image-20210818224658042

image-20210818224711482

image-20210818224728892

image-20210818224743542

高超的技艺

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
//最拉跨的
int Get1Bit(int x)
{
    int sum = 0;
    while(x)
    {
        if(x & 0x01)
        {
            sum += 1;
        }
        x = x >> 1;
    }
    return sum;
}
//面试宝典中
//老师不讲，学生永远不知道
int Get1Bit(int x)
{
    int sum = 0;
    while(x)
    {
        x = x &(x-1);
        sum+=1;
    }
    return sum;
}
//查表方案
int Get1Bit(int x)
{
    int ar[] = {0,1,1,2,1,2,2,3,1,2,2,3,2,3,3,4};
    int sum = 0;
    for(int i = 0;i<sizeof(x)*2;++i)
    {
        sum = sum + ar[x & 0x0f];
        x = x >> 4;
    }
    return sum;
}

这个减1就与原数按位与，每次都会少个1。

image-20210823024356781

计算一个4字节整型的二进制格式中1的个数。

有一位图论的学生，面试时通过此题进入了腾讯。

image-20210823021837556

image-20210823021900711

image-20210823021915500

断位

1
2
3
4
5
6
7
8
9
10
11
12
13
14
struct Node
{
    char a:4;
    unsigned char b:3;
    
    unsigned char c:5;
};
int main()
{
    struct Node x={};
    x.a = 4;
    x.b = 2;
    x.c = 5;
}

刷题

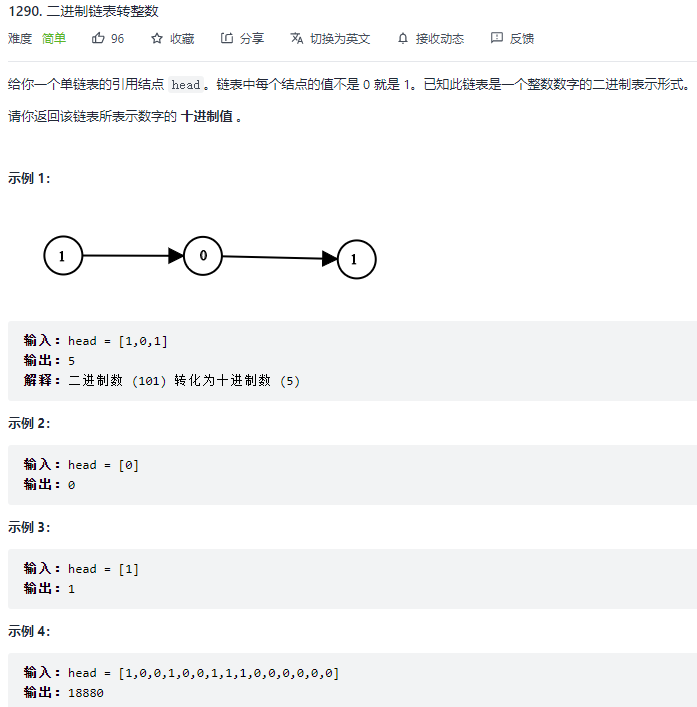
image-20210921200013444

1
2
3
4
5
6
7
8
9
10
11
int getDecimalValue(struct ListNode* head)
{
    int res = 0;
    struct ListNode* p = head;
    while (p != NULL)
    {
        res = res << 1 | p->val;
        p = p->next;
    }
    return res;
}