Redis_dict

发表于2021-07-30更新于2025-09-28阅读次数

引例

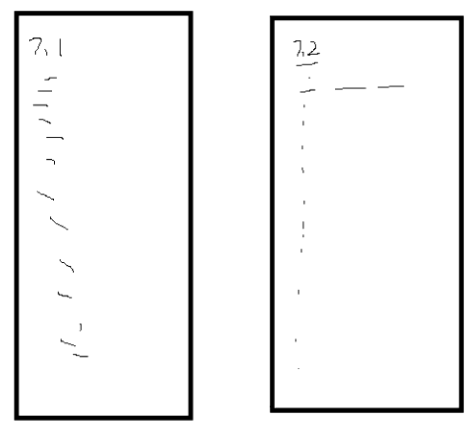
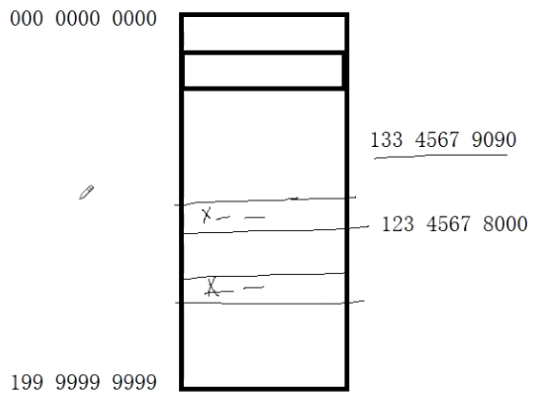
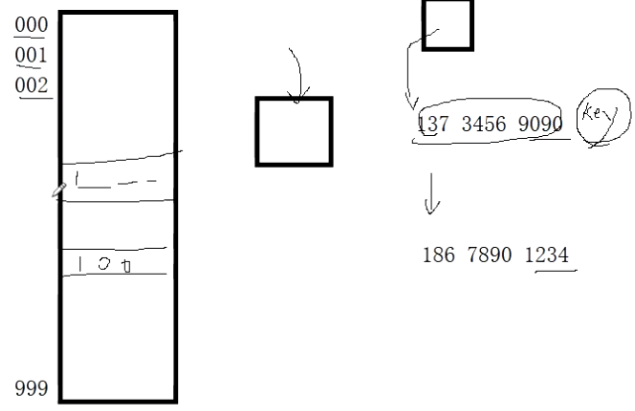
图书馆借书问题，图书馆有成千上万本图书，最初，需要有一个本子记录哪一天学生记录的情况。最初以日期为编号记录某一天来借书的情况。当有人来还书时，需要先问清借书者是几号来借的，然后还要在这天的记录里依次找到具体信息。如果借书者清楚自己是几号借的还好说，但是如果不记得了呢？比如说他只记得好像是上上个月来借的，那么就需要一天一天的从头到尾查找记录，显然效率是低下的。
image-20210807233939705
那么我们可以如此改进：我们搞一个000 0000 0000 ~ 199 9999 9999页的本子，某同学借书时让他提供电话号码，以电话号码为基准记录信息。待还书时，只需要报电话号则可以直接找到记录。但此方法不现实，因为本子太厚，要花费的空间太大。
image-20210807234740133
再改进：做一个1000页的本子，因为电话号码的范围远远大于页数，我们要想办法使电话号码映射到页数，则这个映射方案则称为“哈希函数”。如A同学电话号码为137 3456 9090，可取后三位090，存到90页。B同学电话号码为186 7890 1234，取后三位234，存到234页。
image-20210807235252067
此时又来了一个C同学，电话号码为156 9090 1234，虽然关键码与B同学不一样，但位置信息一样，则称之为“哈希冲突”。

哈希表

什么是哈希表

严蔚敏版本的数据结构教材中指出，在诸如线性表、树结构中，“记录”中结构中的相对位置是随机的，和“记录”的关键字之间不存在确定的关系，因此，在结构中查找记录时需进行一系列和关键字的比较。比如，数组存放的从小到大的10个数据，要用二分查找法找出某value的下标值就需要一直探测。这一类查找方法建立在“比较”的基础上。在顺序查找时，比较的结果为“=”与“≠”两种可能；在折半查找、二叉排序树查找和B树查找时，比较的结果为“<”、“=”和“>”3种可能。查找的效率依赖于查找过程中所进行的比较次数。

我们所向往的理想的情况是希望不经过任何比较，一次存取便能得到所查记录，那就必须在记录的存储位置和它的关键字之间建立一个确定的对应关系f，使每个关键字和结构中一个惟一的存储位置相对应。因而在查找时只要根据这个对应关系f找到给定值K的“像”f(K)便能找到其存储位置。若结构中存在关键字和K相等的记录，则必定在f(K)这个存储位置上，由此不需要比较便可直接取得所查记录。在此我们称这个对应关系f为哈希（Hash）函数，由此思想建立的表称为哈希表。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#include<stdio.h>
#include<assert.h>
#define NIL -1
#define m 13
typedef int KeyType;
struct ElemType
{
  	KeyType key;
    void* ptr;	//value
};
typedef struct
{
    ElemType data[m];
    int cursize;
}HashTable;

image-20210808011308669

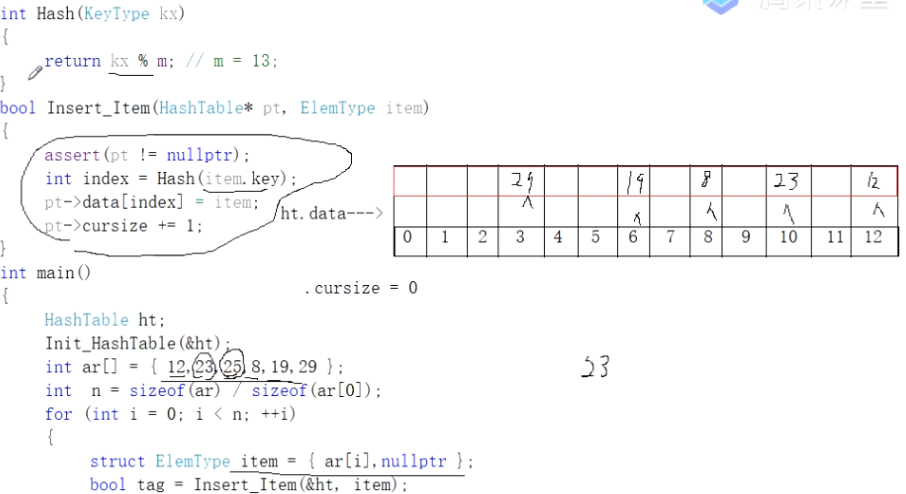
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
void Init_HashTable(HashTable* pt)
{
    assert(pt != nullptr);
    pt->cursize = 0;
    for(int i=0;i<m;++i)
    {
        pt->data[i].key = NIL;
        pt->data[i].ptr = nullptr;
    }
}
int Hash(KeyType kx)
{
    return kx%m;
}
bool Insert_Item(HashTable* pt, ElemType item)
{
    assert(pt != nullptr);
    int index = Hash(item.key);
    pt->data[index] = item;
    pt->cursize += 1;
}
int main()
{
    HashTable ht;
    Init_HashTable(&ht);
    int ar[]={12,23,25,8,19,29};
    int n=sizeof(ar)/sizeof(ar[0]);
    for(int i=0;i<n;++i)
    {
        struct ElemType item = {ar[i],nullptr};
        bool tag = Insert_Item(&ht,item);
    }
}

但是这种Insert_Item函数是有问题的，没有解决哈希冲突问题，比如在插入key为25的元素时会替换掉前期已经插入的key为12的元素。

image-20210808013500159

以下来通过 （增量）线性探测法来解决哈希冲突。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
int Inc(int i)
{
    return i;
}
int Hash_Inc(KeyType kx, int i)
{
    return (Hash(kx) + Inc(i))%m;
}
bool Insert_Item(HashTable* pt, ElemType item)
{
    assert(pt != nullptr);
    for(int i = 0;i<m;++i)
    {
        int index = Hash_Inc(item.key, i);
        if(pt->data[i].key == NIL)//随着Inc更迭，找到一个空位置
        {
            pt->data[index] = item;
            pt->cursize += 1;
            return true;
        }
    }
    return false;
}
1
2
3
4
5
6
7
8
9
10
11
12
int main()
{
    HashTable ht;
    Init_HashTable(&ht);
    int ar[]={12,15,28,23,25,38,36,49,14};
    int n=sizeof(ar)/sizeof(ar[0]);
    for(int i=0;i<n;++i)
    {
        struct ElemType item = {ar[i],nullptr};
        bool tag = Insert_Item(&ht,item);
    }
}

image-20210808015044675

这种线性探测法虽然解决了哈希冲突，但最终的数据分布太堆积化。可以通过平方探测法改善此问题。

1
2
3
4
int Inc(int i)
{
    return i*i;
}

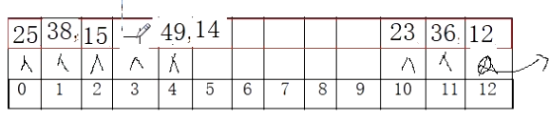
但无论是线性探测法存储还是平方探测法存储，在这种纯顺序表（数组）中实现哈希表会遇到一个严重的问题！即插入数据后，不能轻易删除某一个数据，因为删除了某一数据后，查找另外的数据就会出现数据断层导致不能正常探测。比如下图：如果把3下标的28删除，则查找key为49的元素时，第一次探测49%13=10，23不等于49，第二次探测（线性探测，下标+1），36不等于49，第三次探测，12不等于49，……，直到探测到下标3，发现key值为-1。如果我们停止探测返回，则是错误的；所以我们只能遇到-1不停止继续探测，那么就失去了哈希表的意义，这相当于在查某个key对应的value时有可能把整个表都遍历了一遍。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void* FindValue(HashTable* pt, KeyType kx)
{
    assert(pt != nullptr);
    for(int i = 0;i<m;++i)
    {
        int pos = Hash_Inc(kx,i);
        if(pt->data[pos].key==kx)
        {
            return pt->data[pos].ptr;
        }
        if(pt->data[pos].key==NIL)
        {
            return nullptr;
        }
    }
}

image-20210808020035825

链地址法

所以我们要改变这种存储哈希表的方式，改用链地址法存储。（视频01:27:42）

image-20210808191518194

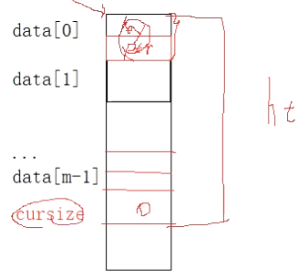
看图设计结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include<stdio.h>
#include<assert.h>
#define m 13
typedef int KeyType;
typedef struct ElemType
{
    KeyType key;
    void* ptr;
}ElemType;
typedef struct HashNode
{
    ElemType data;
    struct HashNode* next;
}HashNode;
typedef struct HashTable
{
    HashNode* table[m];
    int cursize;
}HashTable;

测试代码

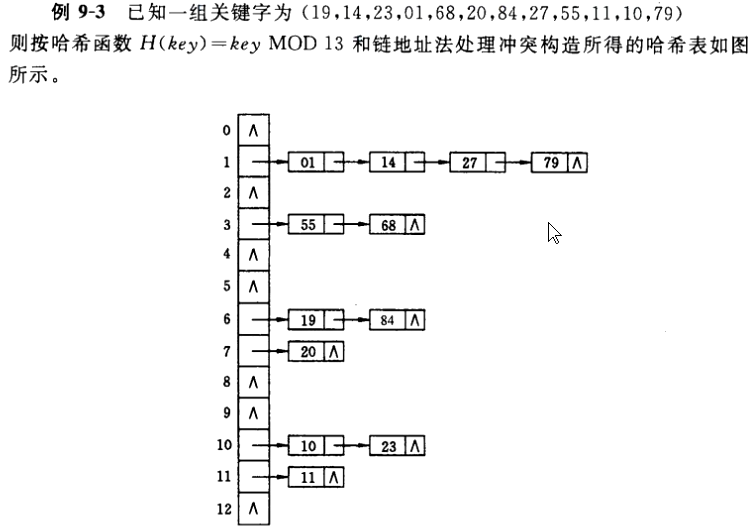
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
int Hash(KeyType kx)
{
    return kx % m;
}
void Init_Hash(HashTable* pt)
{
    assert(pt!=nullptr);
    for(int i = 0;i<m;++i)
    {
        pt->table[i] = nullptr;
    }
    pt->cursize = 0;
}
void Insert_Item(HashTable* pt, ElemType item)//但是此函数没有解决存在相同key时的情况
{
    assert(pt!=nullptr);
    int index = Hash(item.key);
    HashNode* s = (HashNode*)malloc(sizeof(HashNode));
    if(nullptr == s) exit(1);
    s->data = item;
    s->next = pt->table[index];
    pt->table[index] = s;
    pt->cursize += 1;
}
int main()
{
    int ar[]={1,55,19,20,10,11,14,68,84,23,27,79};
    int n = sizeof(ar)/sizeof(ar[0]);
    HashTable ht;
    Init_Hash(&ht);
    for(int i = 0;i<n;++i)
    {
        ElemType elem = {ar[i],nullptr};
        Insert_Item(&ht,elem);
    }
}

API

Init

1
2
3
4
5
6
7
8
9
void Init_Hash(HashTable* pt)
{
    assert(pt != nullptr);
    for(int i = 0;i<m;++i)
    {
        pt->table[i]=nullptr;
    }
    pt->cursize=0;
}

Insert

1
2
3
4
5
6
7
8
9
10
11
12
13
void Insert_Item(HashTable* pt, ElemType item)
{
    assert(pt != nullptr);
    int index = Hash(item.key);
    HashNode* pnode = (HashNode*)malloc(sizeof(*pnode));
    if (nullptr == pnode) exit(1);
    pnode->data = item;//讲外部elem封装到新建结点的数据域
    //以下两步为入表操作，采用头插法，时间复杂度为O(1)，不用判头结点是否为空
    pnode->next = pt->table[index];
    pt->table[index] = pnode;
    
    pt->cursize++;//现有大小+1
}

FindNode

查看字典中是否已存在某key值对应的节点并返回。

1
2
3
4
5
6
7
8
9
10
HashNode* FindNode(HashTable* pt, KeyType kx)
{
	int index = Hash(kx);
	HashNode* p = pt->data[index];
	while (p != nullptr && p->item.key != kx)
	{
		p = p->next;
	}
	return p;
}

Clear

自己写的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//free掉所有节点，HashTable的指针数组数据全赋空
void ClearTable(HashTable* pt)
{
	for (int i = 0;i < m;++i)
	{
		HashNode* p = pt->data[i];
		HashNode* q = nullptr;
		while (p)
		{
			q = p->next;
			free(p);
			pt->cursize--;
			p = q;
		}
		pt->data[i] = nullptr;
	}
}

老师写的

1
2
3
4
5
6
7
8
9
10
11
12
13
void ClearHash(HashTable* pt)
{
    for(int i = 0;i<m;++i)
    {
        while(pt->data[i]!=nullptr)
        {
            HashNode* q = pt->data[i];
            pt->data[i]=q->next;
            free(q);
        }
    }
    pt->cursize=0;
}

Remove

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
//删除某一节点，需用到两个指针变量，一前一后。
void RemoveNode(HashTable* pt, KeyType kx)
{

	int index = Hash(kx);
	HashNode* p = pt->data[index];
	if (p == nullptr) exit(1);//不存在要删除的key的对应节点，因为Table数组此下标的值既然为空则肯定不会有key值相应的节点存在
	HashNode* q = p->next;
	//若删除的节点为头结点，则特殊处理
	if (p->item.key == kx)
	{
		pt->data[index] = q;
		free(p);
	}
	else//
	{
		while (q != nullptr && q->item.key != kx)
		{
			p = p->next;
			q = q->next;
		}
		if (q == nullptr) exit(1);//不存在要删除的key的对应节点，因为遍历这一条链后不存在相同的key值对应的节点。
		else//q->item.key == kx
		{
			p->next = q->next;
			free(q);
		}
	}
	pt->cursize--;
	return;
}

老师写法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
//Remove节点更老套的写法：
bool Remove(HashTable* pt,KeyType kx)
{
    assert(pt!=nullptr);
    int index=Hash(kx);
    HashNode* pr=nullptr;//前驱指针
    HashNode* p=pt->table[index];
    while(p!=nullptr)
    {
        if(p->item.key==kx)
        {
            if(pr!=nullptr)
            {
                pr->next=p->next;
            }
            else
            {
                pt->table[index]=p->next;
            }
            free(p);
            pt->total-=1;
            return true;
        }
        pr=p;
        p=p->next;
    }
    return false;
}

习题

定义大小为100 的整型数组，使用随机函数给数组元素赋值。数值的范围是1 … 100 ，并且不容许重复。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
int* My_NonRepeating_RandArr(int* ar, int n)
{
    assert(ar != nullptr);
    int br[101];
    for (int i = 0;i < n + 1;++i)
    {
        br[i]=0;
    }
    int temp;
    srand(time(NULL));
    int i = 0;
    do
    {
        temp = rand() % 100 + 1;
        if (br[temp] != 1)
        {
            br[temp] = 1;
            ar[i] = temp;
            ++i;
        }
    } while (i<n);
    return ar;
}

如果题中数组大小改为1000000，那么数组开辟空间就很大，如果仍然按照旧的方式去做肯定是对程序不利的。考虑用哈希算法解决！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
#include<stdio.h>
#include<assert.h>
#define m 100
typedef int KeyType;
typedef struct ElemType
{
    KeyType key;
    void* ptr;
}ElemType;
typedef struct HashNode
{
    ElemType data;
    struct HashNode* next;
}HashNode;
typedef struct HashTable
{
    HashNode* table[m];
    int cursize;
}HashTable;
void Init_Hash(HashTable* pt)
{
    assert(pt != nullptr);
    for(int i = 0;i<m;++i)
    {
        pt->table[i]=nullptr;
    }
    pt->cursize=0;
}
void Insert_Item(HashTable* pt, ElemType item)
{
    assert(pt != nullptr);
    int index = Hash(item.key);
    HashNode* pnode = (HashNode*)malloc(sizeof(*pnode));
    if (nullptr == pnode) exit(1);
    pnode->data = item;//讲外部elem封装到新建结点的数据域
    //以下两步为入表操作，采用头插法，时间复杂度为O(1)，不用判头结点是否为空
    pnode->next = pt->table[index];
    pt->table[index] = pnode;
    
    pt->cursize++;//现有大小+1
}
int Hash(KeyType kx)
{
    return kx%m;
}
HashNode* FindValue(HashTable* pt, KeyType kx)
{
    int index = Hash(kx);
    HashNode* p = pt->table[index];
    while(p != nullptr && p->data.key != kx)
    {
        p=p->next;
    }
    return p;
}
int* My_NonRepeating_Hash(int* ar, int n)
{
    assert(ar != nullptr);
    HashTable ht;
    Init_Hash(&ht);
    int temp;
    srand(time(NULL));
    int i = 0;
    do
    {
        temp = rand()* rand() % 1000000 + 1;
        if (FindValue(&ht, temp) == nullptr || *(int*)(FindValue(&ht, temp)->data.ptr) != 1)
        {
            ElemType item = { temp,new int(1) };
            Insert_Item(&ht, item);
            ar[i] = temp;
            ++i;
        }
    } while (i < n);
    return ar;
}
int main()
{
    
}

老师写的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
#include<assert.h>
#define m 13
#define INC	2
typedef int KeyType;
typedef struct
{
    KeyType key;
    void* ptr;
}ElemType;
typedef struct HashNode
{
    ElemType data;
    struct HashNode* next;
}HashNode;
typedef struct HashTable
{
    HashNode** table;
    int capacity;
    int total;
}HashTable;
int Hash(HashTable* pt, KeyType kx)
{
    //return kx % m; //原始不考虑增容的情况下默认%m
    return kx % pt->capacity;
}
void Init_Hash(HashTable* pt)
{
    assert(pt!=nullptr);
    pt->table = (HashNode**)malloc(sizeof(HashNode*)*m);
    if(pt->table == nullptr)exit(EXIT_FAILURE);
    pt->capacity = m;
    for(int i = 0;i<pt->capacity;++i)
    {
        pt->table[i] = nullptr;
    }
    pt->total = 0;
}
HashNode* FindNode(HashTable* pt, KeyType kx)
{
    int index = Hash(pt,kx);
    HashNode* p = pt->table[index];
    while(p != nullptr && p->data.key != kx)
    {
        p=p->next;
    }
    return p;
}
bool Inc(HashTable* pt)//对哈希表的增容操作
{
    int incsize = pt->capacity * INC;//INC为增容系数，默认为2，incsize表示增容后的新大小，为此前哈希表容量的2倍。
    HashNode** newtable = (HashNode**)malloc(sizeof(HashNode*)*incsize);
    if(newtable == nullptr)return false;
    for(int i = 0;i<incsize;++i)
    {
        newtable[i] = nullptr;
    }
    pt->captacity = incsize;
    //以上，开辟新的哈希表完毕，下面要把旧表复制到新表
    int oldsize = pt->capacity;
    for(int i = 0;i<oldsize;++i)
    {
        if(pt->table[i]!=nullptr)
        {
            
        }
    }
}
bool Insert_Item(HashTable* pt, ElemType item)
{
    assert(pt!=nullptr);
    HashNode* p = FindNode(pt,item.key);
    if(p!=nullptr)return false;//哈希表中已存在相同key值的节点
    if(pt->total > pt->capacity && !Inc(pt))//需要增容但没有增容成功
    {
        return false;
    }
    int index 
}

C++就一个东西引用返回，B站的老师永远搞不清楚

Redis字典

字典，又称为符号表(symbol table)、关联数组(associative array)或映射(map)，是一种用于保存键值对(key-value pair)的抽象数据结构。
在字典中，一个键(key)可以和一个值(value)进行关联（或者说将键映射为值），这些关联的键和值就称为键值对。
字典中的每个键都是独一无二的，程序可以在字典中根据键查找与之关联的值，或者通过键来更新值，又或者根据键来删除整个键值对，等等。
字典经常作为一种数据结构内置在很多高级编程语言里面，但Redis所使用的C语言并没有内置这种数据结构，因此 Redis构建了自己的字典实现。
字典在Redis中的应用相当广泛，比如 Redis的数据库就是使用字典来作为底层实现的，对数据库的增、删、查、改操作也是构建在对字典的操作之上的。

与相似结构对比

HashTable是无序的；
Map是有序的；HashMap是无序的，底层有红黑树实现。因此Map效率较低。

字典的实现

Redis的字典使用哈希表作为底层实现，一个哈希表里面可以有多个哈希表节点，而每个哈希表节点就保存了字典中的一个键值对。

哈希表

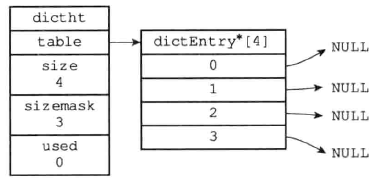
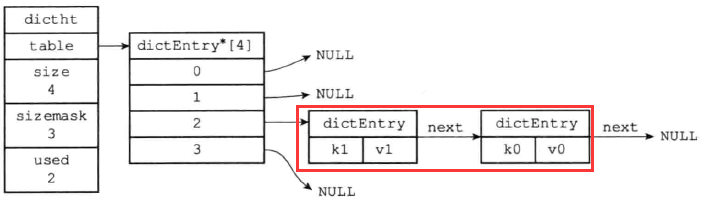
Redis字典所使用的哈希表由dict.h/dictht结构定义：

1
2
3
4
5
6
7
typedef struct dictht
{
    dictEntry** table;//哈希表数组
    unsigned long size;//哈希表大小
    unsigned long sizemark;//哈希表大小掩码，用于计算索引值。总是等于size-1
    unsigned long used;//表中已有节点的数量
}dictht;

成员table的功能是一个数组（指向首元素的指针），数组中的每个元素都是一个指向dict.h/dictEntry结构的指针，每个dictEntry结构保存着一个键值对。

image-20210818030916272

哈希表节点

即dictEntry结构。

1
2
3
4
5
6
7
8
9
10
11
typedef struct dictEntry
{
    void* key;
    union
    {
        void* val;
        uint64_tu64;
        int64_ts64;
    }v;
    struct dictEntry* next;
}dictEntry;

image-20210818031224095

字典

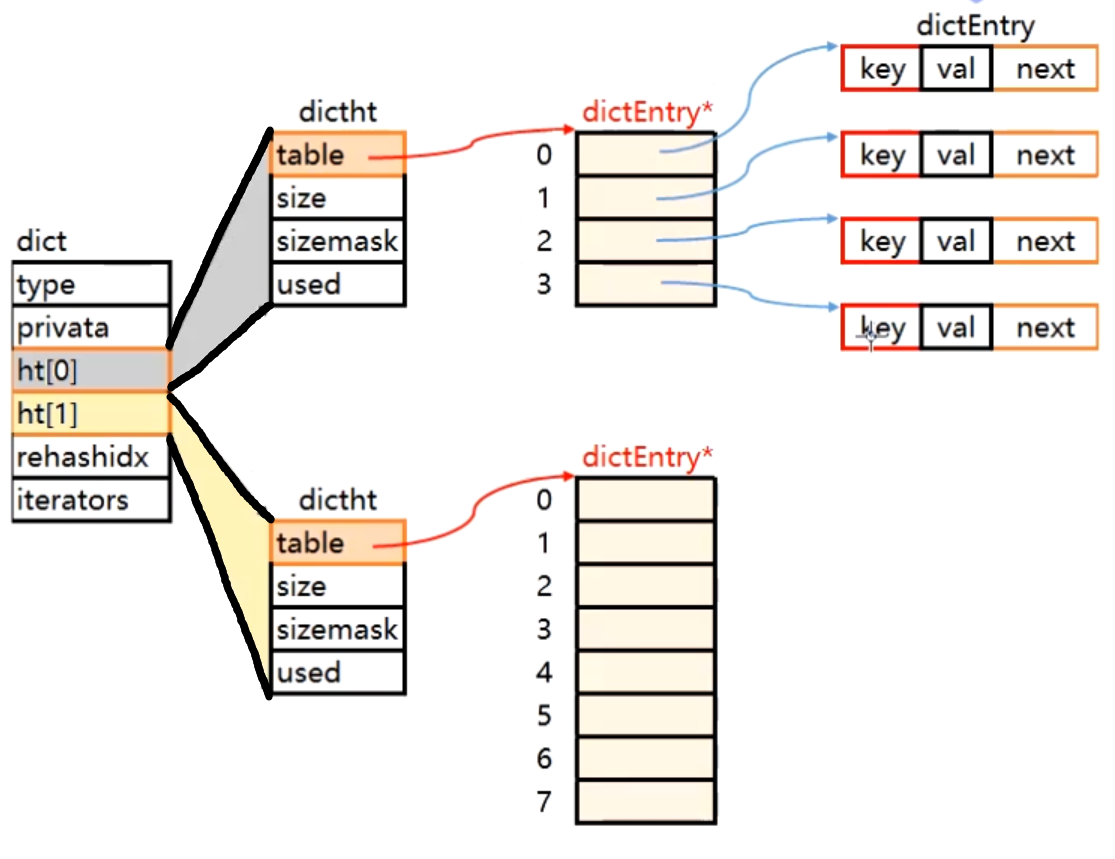
Redis中的字典由dict.h/dict结构表示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
typedef struct dictType 
{
    // 计算哈希值的函数
    unsigned int (*hashFunction)(const void *key);
    // 复制键的函数
    void *(*keyDup)(void *privdata, const void *key);
    // 复制值的函数
    void *(*valDup)(void *privdata, const void *obj);
    // 对比键的函数
    int (*keyCompare)(void *privdata, const void *key1, const void *key2);
    // 销毁键的函数
    void (*keyDestructor)(void *privdata, void *key);
    // 销毁值的函数
    void (*valDestructor)(void *privdata, void *obj);
} dictType;
typedef struct dict
{
    dictType* type;//结构体指针，用于存放特定类型的操作函数
    void* privdata;//私有数据
    dictht ht[2];//内部定义了两个哈希表
    int rehashidx;//当没有在rehash时值为-1
}dict;

image-20210818032212233

面试

  1. 渐进式增容/缩容
  2. 一致性哈希–解决负载均衡的问题。比如登陆项目。一千万个用户同时登陆。
  3. 操作系统一定要开始看了，内存管理、进程管理、线程管理。

dictDelete

  1. 删除第一节点
  2. 删除后个数会少，要处理

time

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/*
 * 返回以毫秒为单位的 UNIX 时间戳
 *
 * T = O(1)
 */
long long timeInMilliseconds(void) 
{
    struct timeval tv;

    gettimeofday(&tv,NULL);
    return (((long long)tv.tv_sec)*1000)+(tv.tv_usec/1000);
}
/* Rehash for an amount of time between ms milliseconds and ms+1 milliseconds */
/*
 * 在给定毫秒数内，以 100 步为单位，对字典进行 rehash 。
 *
 * T = O(N)
 */
int dictRehashMilliseconds(dict *d, int ms) 
{
    // 记录开始时间
    long long start = timeInMilliseconds();
    int rehashes = 0;

    while(dictRehash(d,100)) {
        rehashes += 100;
        // 如果时间已过，跳出
        if (timeInMilliseconds()-start > ms) break;
    }

    return rehashes;
}