C++中的智能指针定义于<memory>中。
内容
- RAII
- auto_ptr
- unique_ptr
- shared_ptr
- weak_ptr
RAII
堆上空间进行自动化管理,利用对象自动析构的机制。
auto_ptr
这是旧版本的智能指针,在C++11之后被废弃。
- 不能使用同一个裸指针赋值/初始化多个
auto_ptr。
- 拷贝构造和等号运算符,会将源智能指针置空。
- release(): 返回当前指向的地址(存到tmp中),并将当前智能指针置空
- reset(): 将当前智能指针指向的内存释放,指针置空。
问题
拷贝构造函数意义不明确
- 如果拷贝构造按浅拷贝形式进行,则会导致重复析构,崩溃。
- 如果拷贝构造按转移资源进行,则会导致意想不到的严重后果:如以下代码,在调用fun函数按值传入
my_auto_ptr对象时,调用拷贝构造,拷贝构造释放自己的拥有权,给了apx。在fun函数外再找原指针时,原对象的指针信息已丢失。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| class my_auto_ptr
{
public:
my_auto_ptr(const my_auto_ptr& op)
: _Owns(op._Owns), _Ptr(op.release())
{
}
_Ty* release() const
{
_Ty* tmp = NULL;
if (_Owns)
{
_Owns = false;
tmp = _Ptr;
_Ptr = NULL;
}
return tmp;
}
};
void fun(my_auto_ptr<Object> apx)
{
int x = apx->Value();
cout << x << endl;
}
int main()
{
my_auto_ptr<Object> pobja(new Object(10));
fun(pobja);
int a = pobja->Value();
cout << a << endl;
}
|
赋值重载意义不明确
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| class my_auto_ptr
{
public:
my_auto_ptr & operator=(const my_auto_ptr& _Y)
{
if(this == & _Y)return *this;
if(_Owns){delete _Ptr;}
_Owns = _Y._Owns;
_Ptr = _Y.release();
}
_Ty* release() const
{
_Ty* tmp = NULL;
if (_Owns)
{
_Owns = false;
tmp = _Ptr;
_Ptr = NULL;
}
return tmp;
}
};
void fun(my_auto_ptr<Object> apx)
{
int x = apx->Value();
cout << x << endl;
}
int main()
{
my_auto_ptr<Object> pobja(new Object(10));
fun(pobja);
int a = pobja->Value();
cout << a << endl;
}
|
unique_ptr
以下是传统的不使用智能指针的写法。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| #include <iostream>
#include <memory>
class Test
{
public:
Test(void)
{
std::cout << "Test()" << std::endl;
}
~Test()
{
std::cout << "~Test()" << std::endl;
}
void show(void) const
{
std::cout << "show()" << std::endl;
}
};
void foo()
{
Test * test = new Test;
test->show();
delete test;
test = nullptr;
}
int main()
{
foo();
return 0;
}
|
如今不推荐这么写了,
如何实现让test对象一出foo函数就自动析构呃呢?使用智能指针解决。
1
2
3
4
5
6
| void foo()
{
std::unique_ptr<Test> test{ new Test };
test->show();
}
|
用智能指针管理时,就不用手动释放new出来的Test对象了,因为智能指针是在栈上建立的,函数调用结束后栈帧析构时,智能指针就会自动析构,从而把绑定的对象也析构。
特性:unique
- 把拷贝构造函数禁用了。
- 如果想要迁移原智能指针,可以用move
1
2
3
4
5
6
7
8
9
| void foo()
{
std::unique_ptr<Test> test{ new Test };
std::unique_ptr<Test> test2 = std::move(test);
if (test)
test->show();
if (test2)
test2->show();
}
|
方法
智能指针对象的->对应的是其持有对象的方法。
.出来的方法才是其本身拥有的方法。
release(不析构旧对象)
1
| pointer release() noexcept;
|
释放管理权,返回其持有对象的指针。
智能指针不再管理该对象,程序员需要自己处理析构。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| class Test
{
public:
Test(void)
{
std::cout << "Test()" << std::endl;
}
~Test()
{
std::cout << "~Test()" << std::endl;
}
void show(void) const
{
std::cout << "show()" << std::endl;
}
private:
int _v{ 5 };
};
void foo()
{
std::unique_ptr<Test> test{ new Test };
Test* raw_ptr = test.release();
if (test)
test->show();
delete raw_ptr;
raw_ptr = nullptr;
}
int main()
{
foo();
return 0;
}
|
reset(会析构旧对象)
接收一个同类对象的指针,或nullptr。
原本的智能指针不再指向旧的对象地址,转而指向新的对象地址。
- 如果旧对象没有其他智能指针引用,则析构旧对象
- 指向新对象或nullptr
1
2
3
4
5
6
7
| void foo()
{
std::unique_ptr<Test> test{ new Test };
test.reset(new Test);
if (test)
test->show();
}
|
自实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| template <typename T>
class SmartPtr
{
public:
SmartPtr(nullptr_t) : _t{ nullptr } {}
SmartPtr(void) : _t{ nullptr } {}
SmartPtr(T* t) : _t{ t } {}
~SmartPtr()
{
if (_t)
{
delete _t;
_t = nullptr
}
}
private:
T* _t;
};
int main()
{
SmartPtr test{ new Test };
}
|
处理对象数组
用模板特化。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| template <typename T>
class SmartPtr<T[]>
{
public:
SmartPtr(T* t) : _t{ t } {}
~SmartPtr()
{
if (_t)
{
delete [] _t;
_t = nullptr;
}
}
private:
};
void foo()
{
SmartPtr<Test[]> test{ new Test[5] };
}
|
->重载
->的重载比较有意思,我们想要实现的效果是smartPtr->objFunc(),而->先返回的是obj*,本来应该还需要一个->才正确,但系统默认一个->就懂你的意思。
1
2
3
4
5
6
7
8
9
10
11
12
| template <typename T>
class SmartPtr
{
public:
T* operator-> (void)
{
return _t;
}
private:
};
|
bool运算符重载
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| template <typename T>
class SmartPtr
{
public:
operator bool(void)
{
return _t;
}
private:
};
void foo()
{
SmartPtr<Test> test{ new Test };
if (test)
test->show();
}
|
unique的转移
- 禁用拷贝构造
- 提供右值引用拷贝构造
- 实现一个release方法,在右值引用拷贝构造中复用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| template <typename T>
class SmartPtr
{
public:
SmartPtr(SmartPtr const&) = delete;
SmartPtr(SmartPtr && other) noexcept
{
_t = other.release();
}
T* release()
{
auto t = _t;
_t = nullptr;
return t;
}
private:
};
void foo()
{
SmartPtr<Test> test{ new Test };
SmartPtr<Test> test2 = std::move(test);
if (test)
test->show();
if (test2)
test2->show();
}
|
shared_ptr
多个智能指针共享一个对象。
支持拷贝构造。
某个shared_ptr析构时,所持有的对象不会析构,直到此对象没有其他shared_ptr引用。这是用内部依赖的引用计数机制实现的。
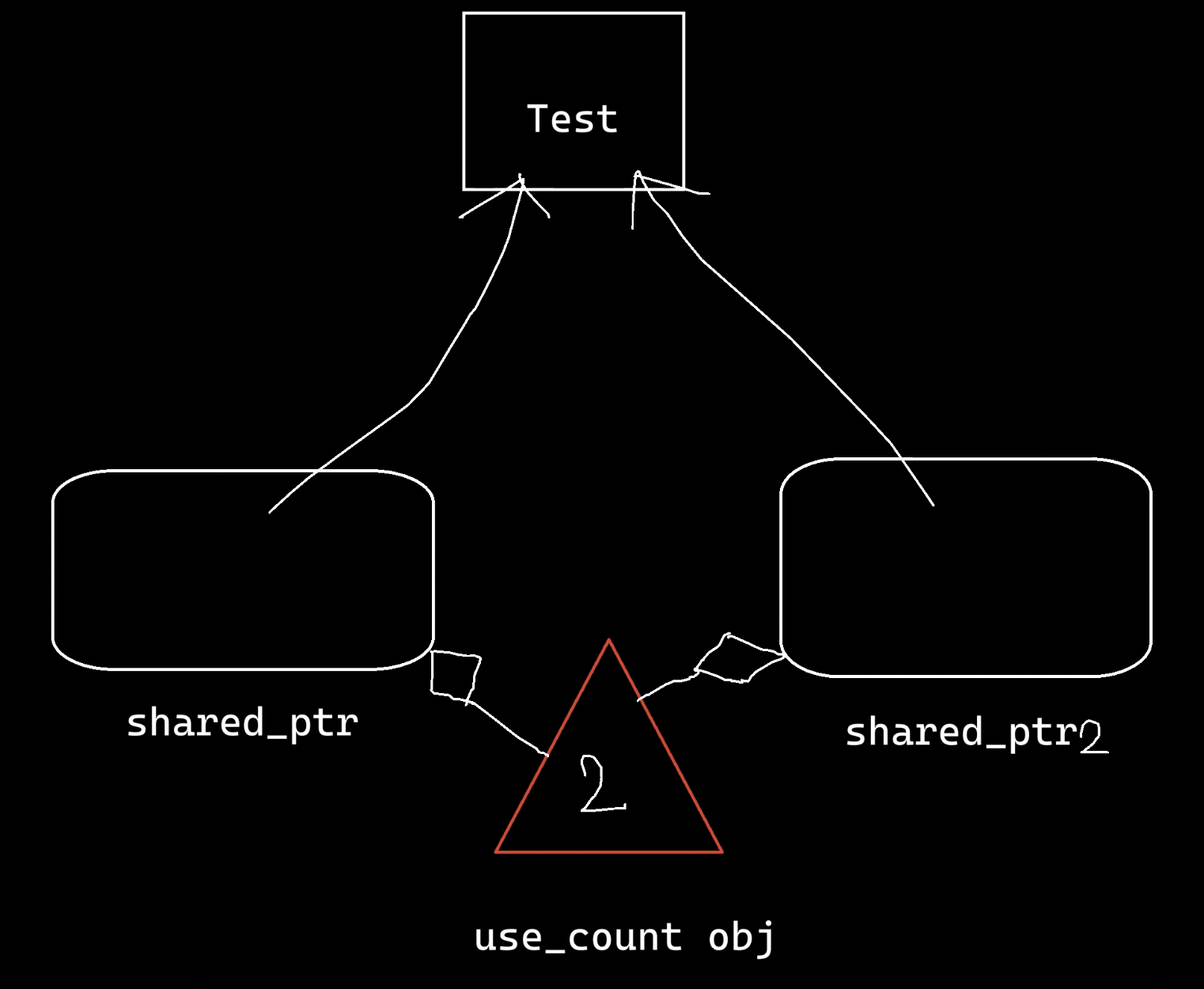
两种构建方式
1
2
3
4
5
| int main()
{
std::shared_ptr<Object> op1(new Object(10));
std::shared_ptr<Object> op2(std::make_shared<Object>(10));
}
|
方法
没有release,只有reset。
可以通过reset(nullptr)或reset()达到release的效果。
use_count
1
2
3
4
5
| void foo()
{
std::shared_ptr<Test> test(new Test);
std::cout << test.use_count() << std::endl;
}
|
owner_before
1
2
3
4
5
6
7
8
| void foo()
{
std::shared_ptr<Test> test(new Test);
std::shared_ptr<Test> test2 = test;
test.reset();
bool is_true = test.owner_before(test2);
is_true = test2.owner_before(test);
}
|
对被reset的对象test来说,判断是不是之前test2所持对象的拥有者。
要想返回true需要满足:
- test已经被reset
- 指定的智能指针确实是test之前指向的对象
1
2
3
4
5
6
7
| void foo()
{
std::shared_ptr<Test> test(new Test);
std::shared_ptr<Test> test2 = test;
bool is_true = test.owner_before(test2);
}
|
应用场景
返回一个指针时。即,用于函数间传递指针。
省去了程序员去判断何时需要析构的难题。
1
2
3
4
5
6
7
8
9
10
11
12
13
| std::shared_ptr<Test> foo()
{
std::shared_ptr<Test> test(new Test);
test->show();
return test;
}
int main()
{
std::shared_ptr<Test> test = foo();
if (test)
test->show();
return 0;
}
|
weak_ptr
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
| class B;
class A
{
public:
A(void)
{
std::cout << "A()" << std::endl;
}
~A()
{
std::cout << "~A()" << std::endl;
}
void set_b(std::shared_ptr<B> b)
{
_b = b;
}
private:
std::shared_ptr<B> _b;
};
class B
{
public:
B(void)
{
std::cout << "B()" << std::endl;
}
~B()
{
std::cout << "~B()" << std::endl;
}
void set_a(std::shared_ptr<A> a)
{
_a = a;
}
private:
std::shared_ptr<A> _a;
};
void bar()
{
std::shared_ptr<A> a(new A);
std::shared_ptr<B> b(new B);
a->set_b(b);
b->set_a(a);
}
int main()
{
bar();
return 0;
}
|
上面程序将输出:
意味着A、B对象在最后没有被析构,造成内存泄漏。
本身a、b是一个引用计数。
又因为两个类内部都存在另一个类对象的shared_ptr指针,那么a、b的引用计数又会各自加1变成2。
bar函数调用结束后智能指针a、b析构,但引用计数只减1,无法归零,都在等对方先析构,形成了僵局。
因此当多方内部可能存在交叉、互相引用对方的shared_ptr时,需要改其为一种不会增加引用计数的特殊指针。则weak_ptr应运而生。
1
2
3
4
5
6
7
8
| void bar()
{
std::shared_ptr<A> a(new A);
std::weak_ptr<A> w_a = a;
std::cout << a.use_count << std::endl;
std::cout << w_a.count << std::endl;
}
|
weak_ptr不能直接管理对象。而是可以通过一个已经存在的shared_ptr赋值。
此时weak_ptr作为一个观察者。不能直接引用对象。
想调用的时候,通过以下方法:
方法
- expired用于判断此
weak_ptr是否过期了。
- lock用于把
weak_ptr升级为一个shared_ptr。lock锁定是为了防止在提升等级的期间指针过期,但是取出来之后仍有可能过期,因此需要先if判断取出的指针是否为空。
- 也可以直接lock,但是expired比lock代价小,通过先判断是否过期从而可能省略代价大的lock。
1
2
3
4
5
6
7
8
9
10
11
12
| void bar()
{
std::shared_ptr<A> a(new A);
std::weak_ptr<A> w_a = a;
if(!w_a.expired())
{
if(std::shared_ptr<A> a2 = w_a.lock())
{
a2->show();
}
}
}
|
A、B正确的定义
只需要一方的内部的shared_ptr降级定义为weak_ptr即可解决僵局。
以下,将B内部的引用A的智能指针成员变量改为弱指针。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
| class B;
class A
{
public:
A(void)
{
std::cout << "A()" << std::endl;
}
~A()
{
std::cout << "~A()" << std::endl;
}
void show() const
{
std::cout << "A::show()" << std::endl;
}
void set_b(std::shared_ptr<B> b)
{
_b = b;
}
void show_b() const;
private:
std::shared_ptr<B> _b;
};
class B
{
public:
B(void)
{
std::cout << "B()" << std::endl;
}
~B()
{
std::cout << "~B()" << std::endl;
}
void show() const
{
std::cout << "B::show()" << std::endl;
}
void set_a(std::shared_ptr<A> a)
{
_a = a;
}
void show_a() const
{
if(!_a.expired())
{
if(auto a = _a.lock())
{
a->show();
}
}
}
private:
std::weak_ptr<A> _a;
};
void A::show_b() const
{
if (_b)
{
_b->show();
}
}
void bar()
{
std::shared_ptr<A> a(new A);
std::shared_ptr<B> b(new B);
a->set_b(b);
b->set_a(a);
a->show_b();
b->show_a();
}
int main()
{
bar();
return 0;
}
|
正确的输出:
1
2
3
4
5
6
| A()
B()
B::show()
A::show()
~A()
~B()
|
