输入以下命令,可以看到全部进程。
1 | ps -aux | less |
下面是FreeBSD的 Unix 系统的测试结果:
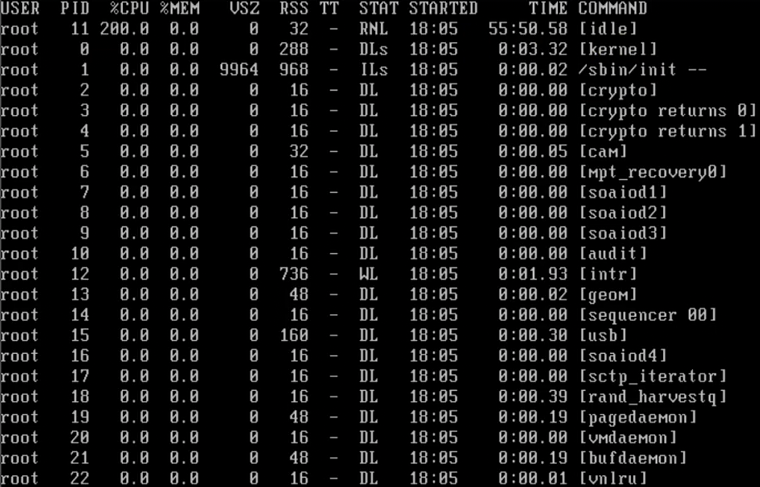
0 号进程为[kernel]。(测试的Ubuntu Linux 系统没有显示 0 号进程)
1号进程为/sbin/init。用于初始化。
[ctypto]用于加密。
有一个特殊的[idle]进程,用于空闲时的调度。某个进程时间片结束,则把权力上交[idle]。由[idle]决定下一次调用谁。
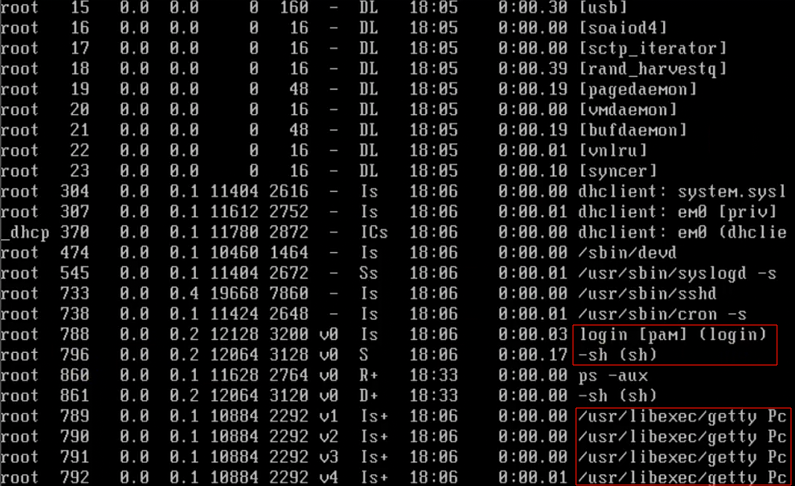
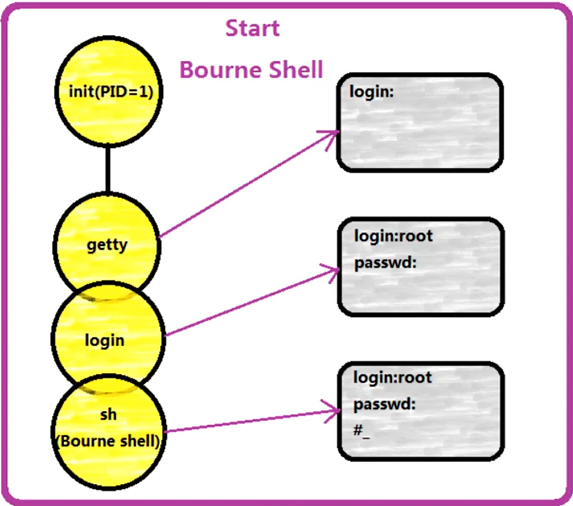
Unix 系统有多个 getty,是终端程序。一旦有哪个人登录,其中一个 getty 就负责调用 login(登陆器),用于登录相关。
如果用户名、密码匹配,最终就会打开Shell。