想用windows主机ssh连接虚拟机,连不上。
确保 SSH 服务已安装并运行
虽然Ubuntu系统自带了ssh,但是这是客户端的,服务端的openssh-server没有安装。
1 | # 检查服务状态 |
检查SSH端口监听
1 | sudo netstat -tuln | grep :22 |
- 正常应显示:
tcp 0 0 0.0.0.0:22 0.0.0.0:* LISTEN - 若未监听,修改配置:
sudo nano /etc/ssh/sshd_config
确保存在:
1 | Port 22 |
重启SSH服务
1 | sudo systemctl restart ssh |
VSCode远程连接
在Extensions中搜索Remote,安装Remote Development。
之后左边就会多出一个选项:
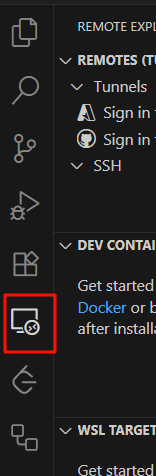
点击后,在边栏右上角选择Remotes(SSH)
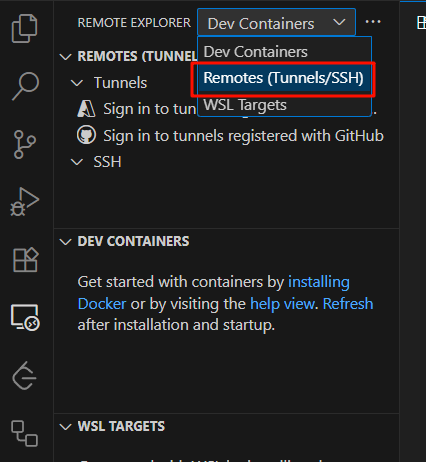
然后点SSH栏右边的齿轮。
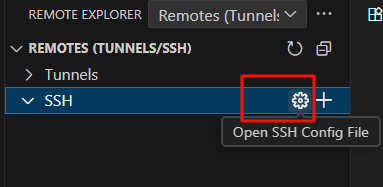
上边栏就会出现:
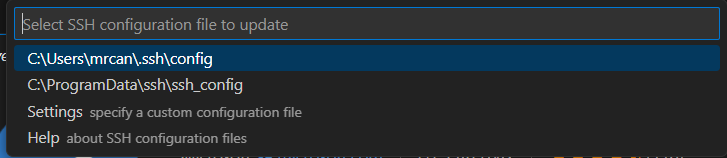
我们选择第一个,也是Windows下当前用户默认的ssh配置文件夹。
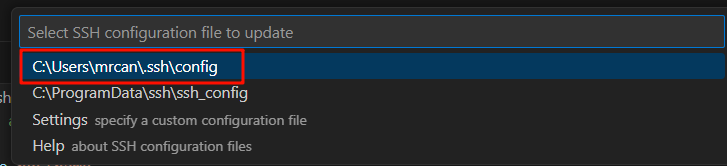
在里面配置远程主机的连接信息
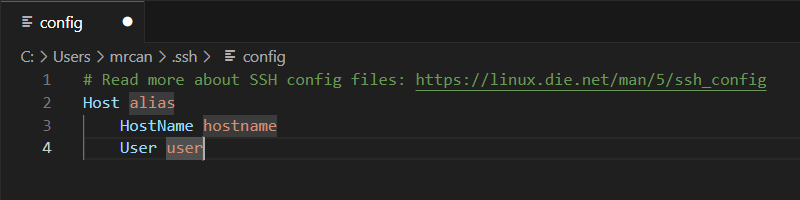
Host指主机名,Linux中@后面的就是。

HostName指ip地址。Linux下ifconfig可以查看。
User指@前面的。
保存文件之后,左边栏就会出现:
SSH远程连接虚拟机 怎么用公钥免除每次登录输入密码的烦恼
服务器存放公钥。
终端存放私钥。
生成密钥对(主机操作)
打开终端(Windows 使用 PowerShell 或 CMD;Mac/Linux 用系统终端)
生成密钥:
1 | ssh-keygen -t ed25519 -C "your_email@example.com" # 推荐 ed25519 |
按提示完成(默认保存位置 ~/.ssh/id_ed25519)
复制公钥到虚拟机的authorized_keys
方法一:自动复制(推荐)(主机操作)
1 | ssh-copy-id -i ~/.ssh/id_ed25519.pub user@vm_ip |
方法二:手动复制
1 | cat ~/.ssh/id_ed25519.pub # 查看主机上的公钥内容 |
配置主机的VSCode
按 F1 > 选择 Remote-SSH: Connect to Host...
选择 Configure SSH Hosts... > 添加配置:(其实是帮你打开~/.ssh/config)
1 | Host MyVM # 自定义别名 |
保存配置文件(通常是 ~/.ssh/config)
常见问题解决
- 权限错误:
chmod 600 ~/.ssh/config # 确保本地 config 文件权限正确 - 服务端配置检查:
- 确认虚拟机
/etc/ssh/sshd_config包含:
PubkeyAuthentication yes AuthorizedKeysFile .ssh/authorized_keys - 重启 SSH 服务:
sudo systemctl restart sshd
- 确认虚拟机
- 调试连接:
ssh -Tv user@vm_ip # -v 查看详细日志
✅ 成功标志:使用
ssh user@vm_ip或 VSCode 连接时无需输入密码即可登录。
遇到问题建议检查两边日志(本地终端 debug 信息或虚拟机/var/log/auth.log)