同时启用两个网卡时如何分流
1 | Ethernet adapter K20 Pro: |
自己的网卡A的网关为192.168.175.219,校园网网卡B的网关为172.21.15.254
- 输入
route print我们能看到本机目前的路由表 - 使用
route delete删除所有0.0.0.0的路由,也就是默认设置,删除默认路由后无法上网。1
2route delete 0.0.0.0
route delete ::/0 - 添加路由表,指定使用网卡B访问特定的IP。设置完后因为我们把默认路由删了,所有就只能访问该地址。
1
route -p add 172.30.201.2 mask 255.255.255.0 172.21.15.254 METRIC 1
- -p 是为了设置为静态永久路由,防止重启时配置消失
- add 添加路由
- 1.1.1.1 指定网卡访问的IP
- 255.255.255.0是网关掩码
- 172.21.15.254指定使用网卡B的网关访问该地址
- METRIC 跃点数,跃点数越小优先级越高,范围1~9999,默认就是1
- 设置默认路由,恢复上网
- 设置校园网卡B的默认路由,跃点数为200,指定IP走默认路由,才能上校园网
1
2route -p add 0.0.0.0 mask 0.0.0.0 172.21.15.254 METRIC 200
route -p add ::/0 mask ::/0 fe80::21b:53ff:fe4a:997f METRIC 200 - 现在网卡B上不了非校园网,所以要设置网卡B的默认路由,跃点数为100,要比200小。因此默认使用网卡A上网,而不是网卡B。
1
2route -p add 0.0.0.0 mask 0.0.0.0 192.168.173.248 METRIC 100
route -p add ::/0 mask ::/0 fe80::f435:31ff:fe10:28af METRIC 100 - 此时网卡A和B同时使用时优先使用网卡A。
- 设置校园网卡B的默认路由,跃点数为200,指定IP走默认路由,才能上校园网
- 如果设置出问题了请用下面命令进行解决。
1
2
3
4NETSH INT IP RESET (重置IP设置)
NETSH WINSOCK RESET (重置网络设置)
NETSH WINHTTP RESET PROXY (重置代理设置)
IPCONFIG /FLUSHDNS (刷新DNS缓存)
校园网网址
| 网址 | IP |
|---|---|
| lgn.bjut.edu.cn | 172.30.201.2 |
| lgn6.bjut.edu.cn | [2001:da8:216:30c9::a] |
| my.bjut.edu.cn | 172.21.94.12 |
OpenWrt的配置
为了正确使用IPV6。
首先给迷你主机刷机,安装OpenWrt系统。
参考大河李斯特视频工作室
注意手边需要有一个显示器、有线键盘,用于进PE刷机、显操作终端界面。
可以在刷机后进OpenWrt系统后:
- 设置root管理员密码
1 | passwd |
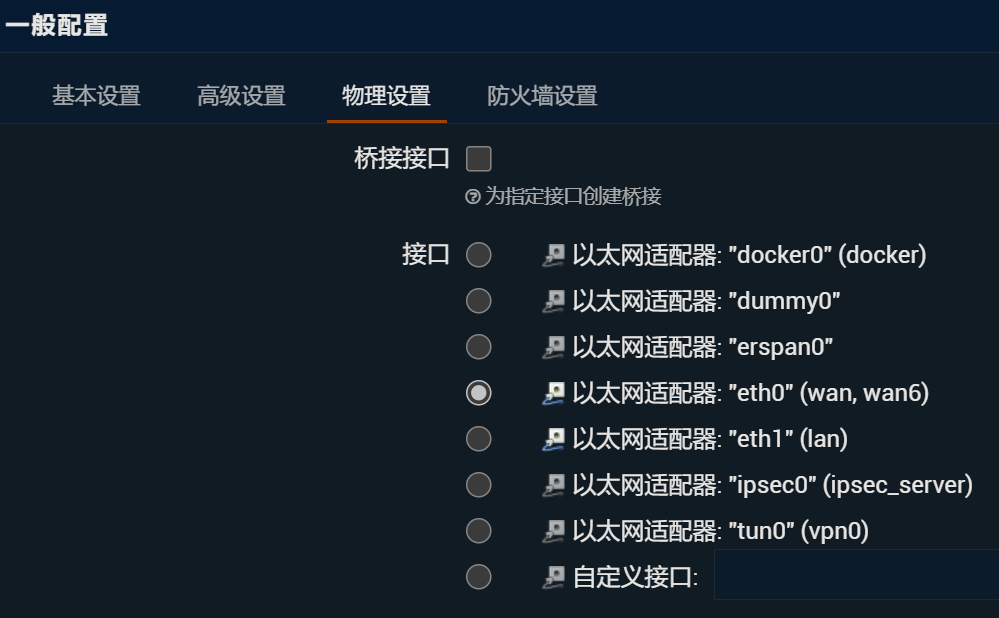
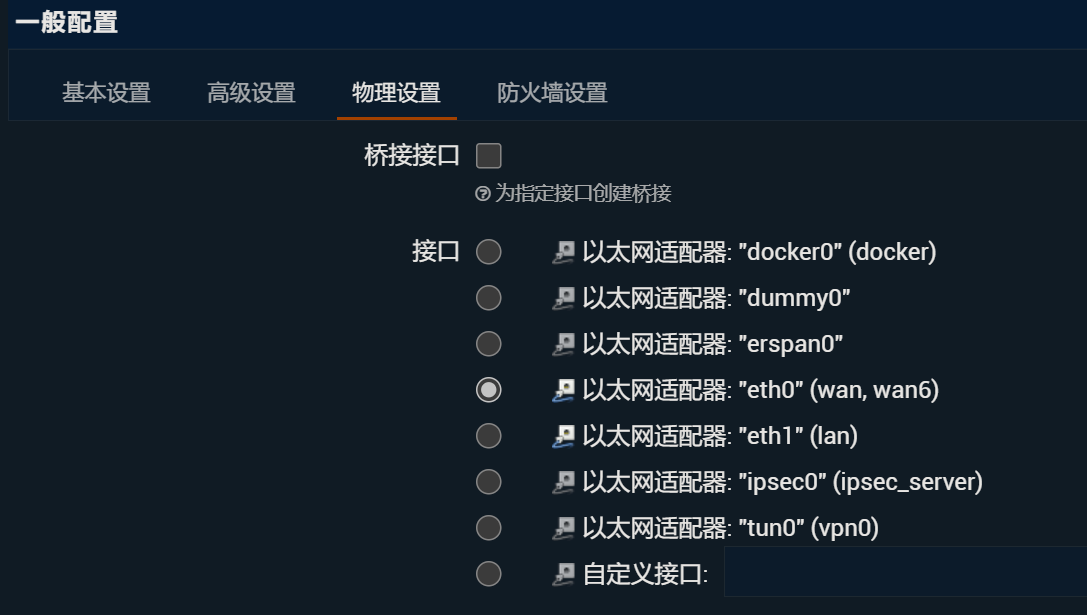
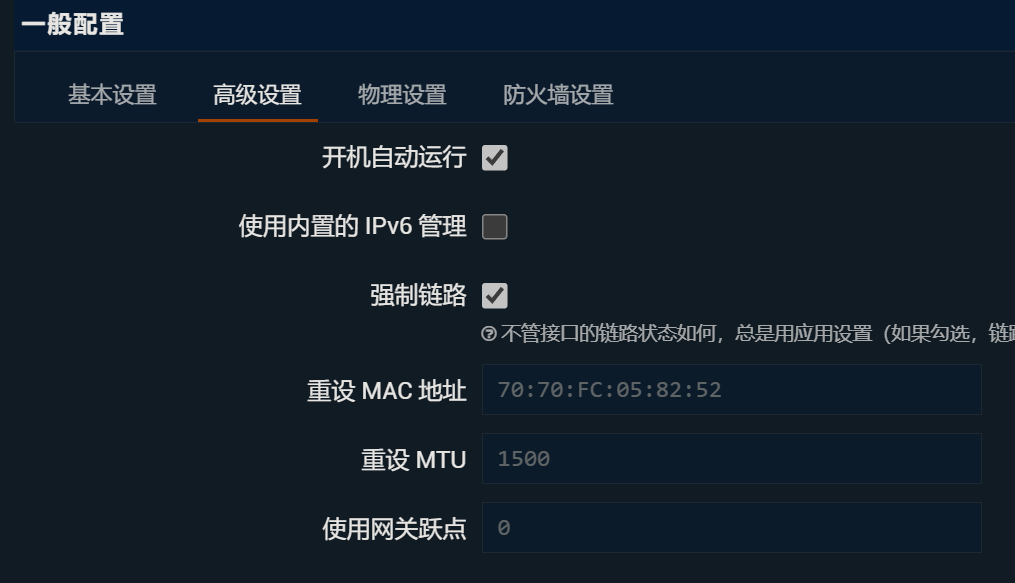
- 修改wan、lan接口号。建议把wan、wan6设置为eth0,lan设置为eth1。
1 | vim /etc/config/network |
- 设置完后reboot。lan口网线插入主PC终端或者AP路由器即可在终端访问
192.168.5.1以远程操作OpenWrt了。
1 | reboot |
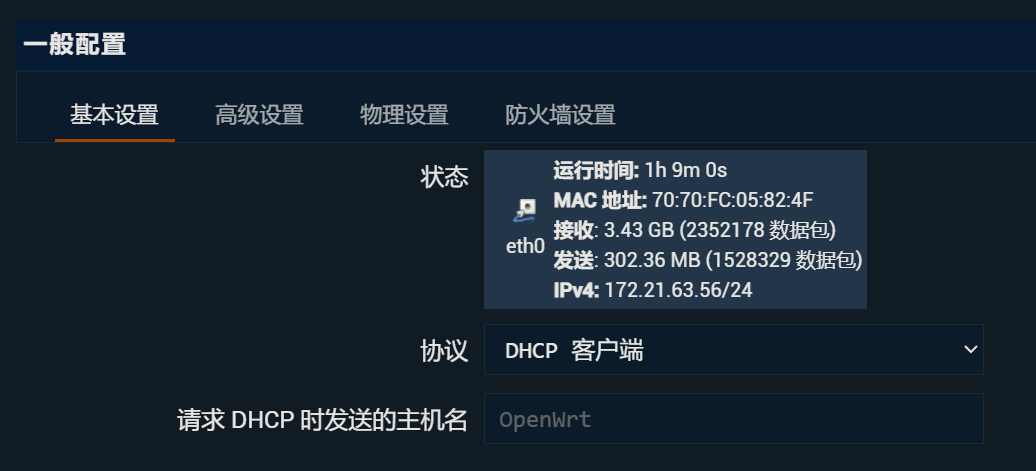
网络-接口配置
WAN口配置如下:
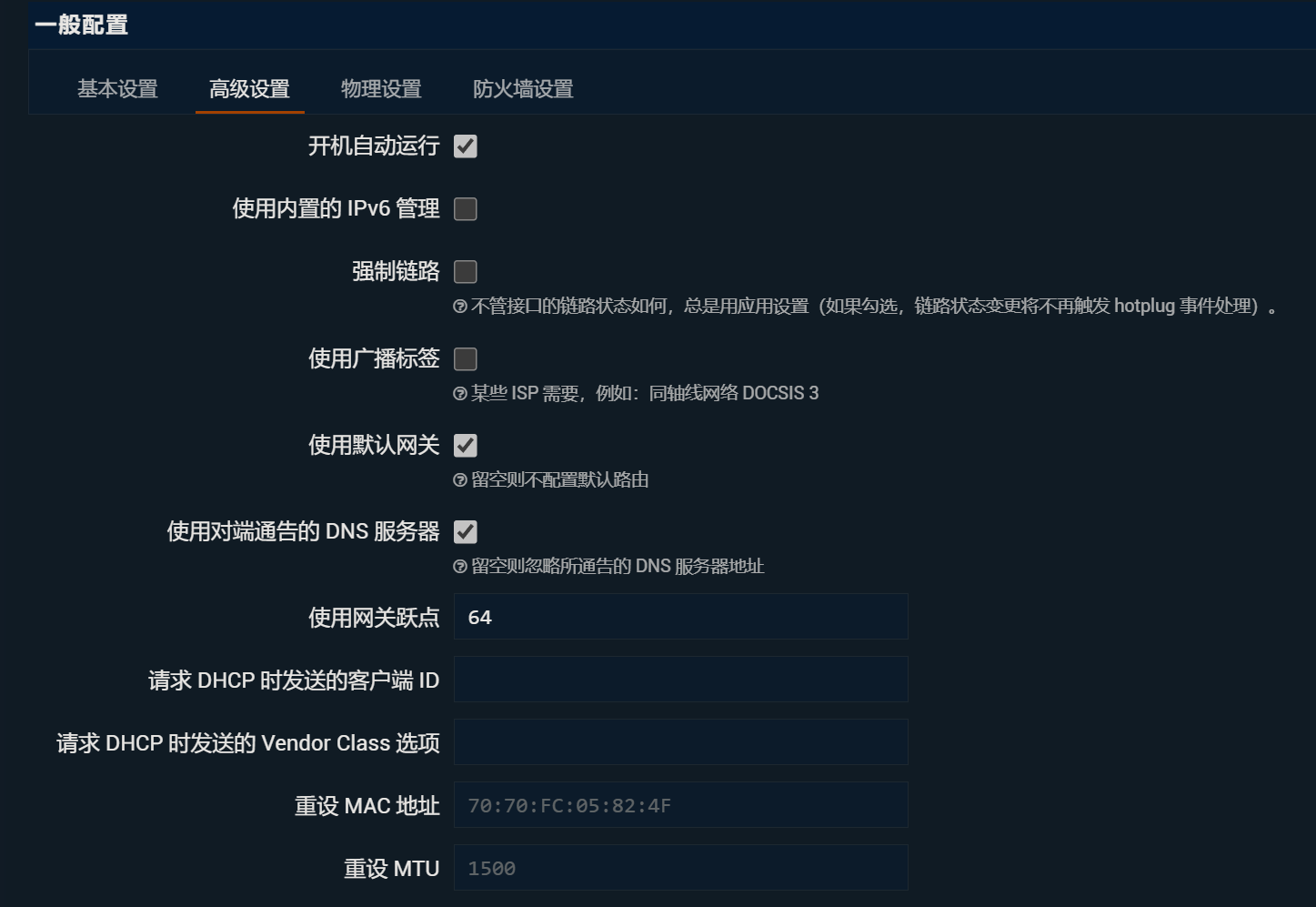
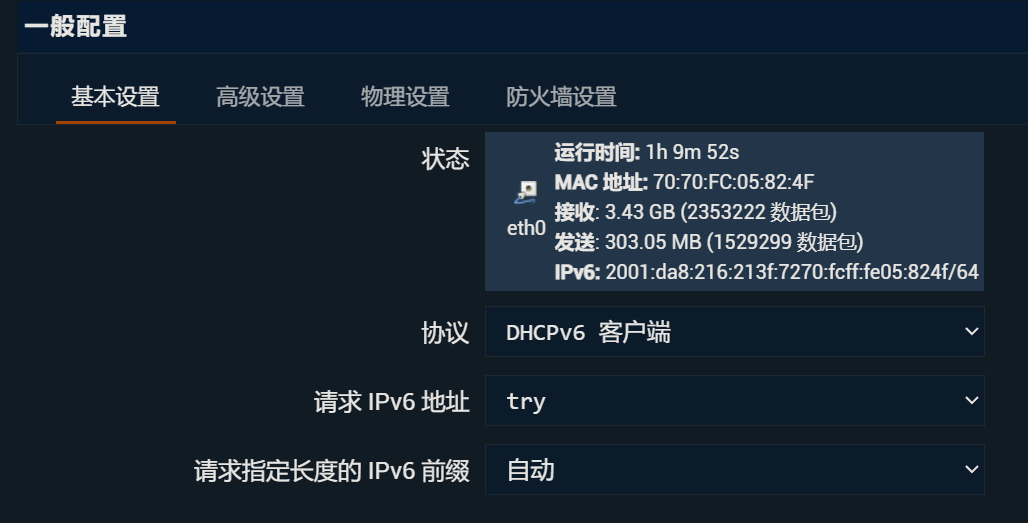
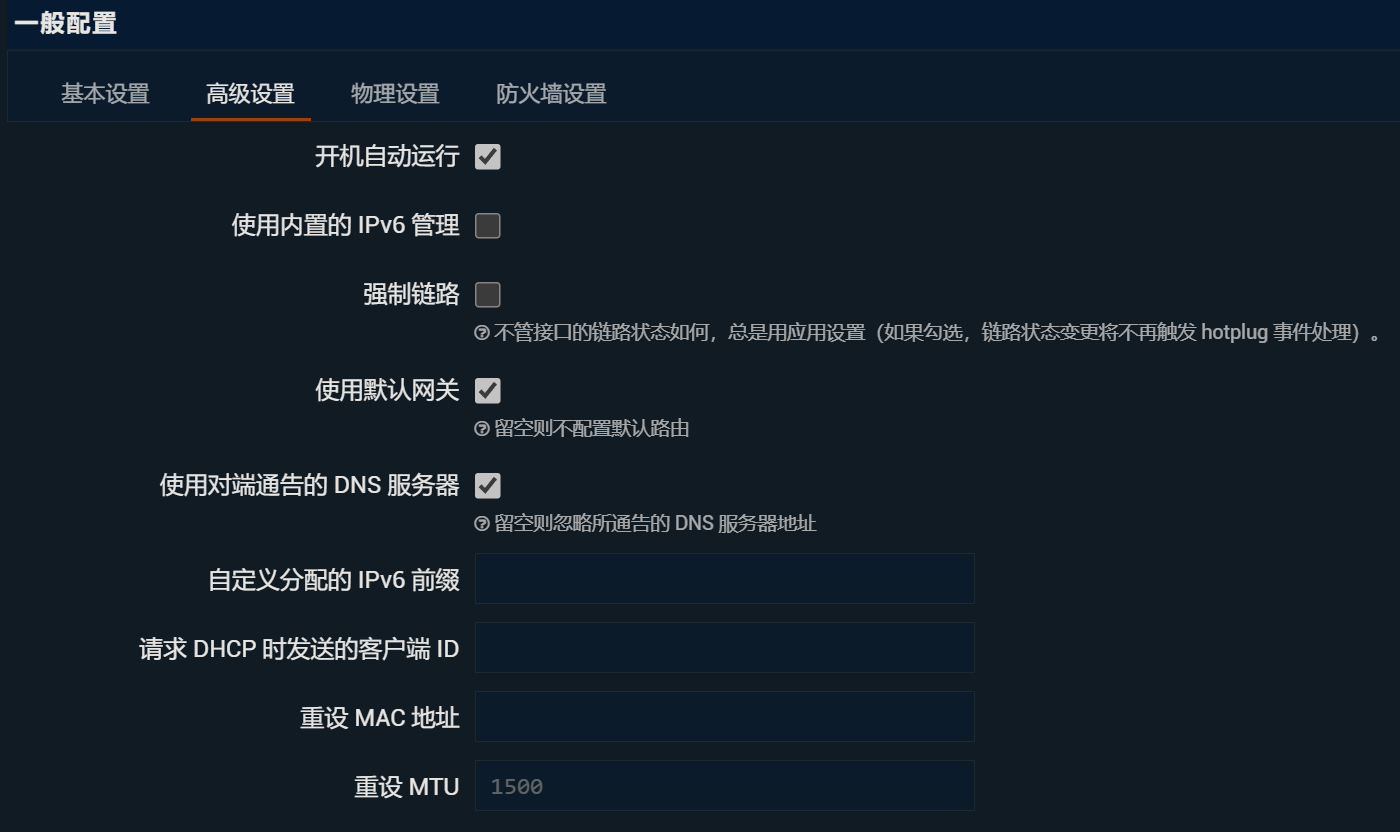
WAN6口配置如下:
LAN口设置如下:
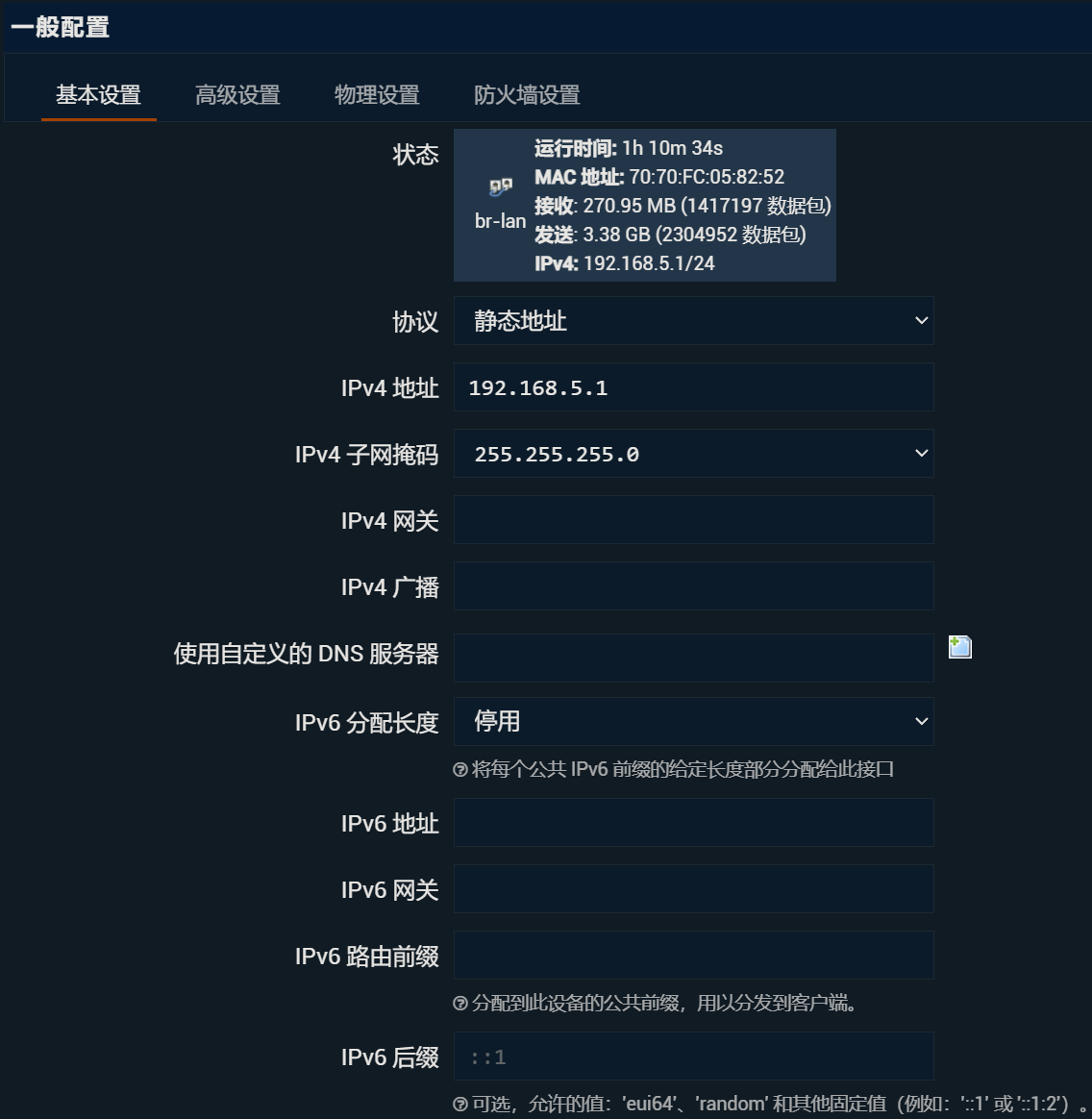
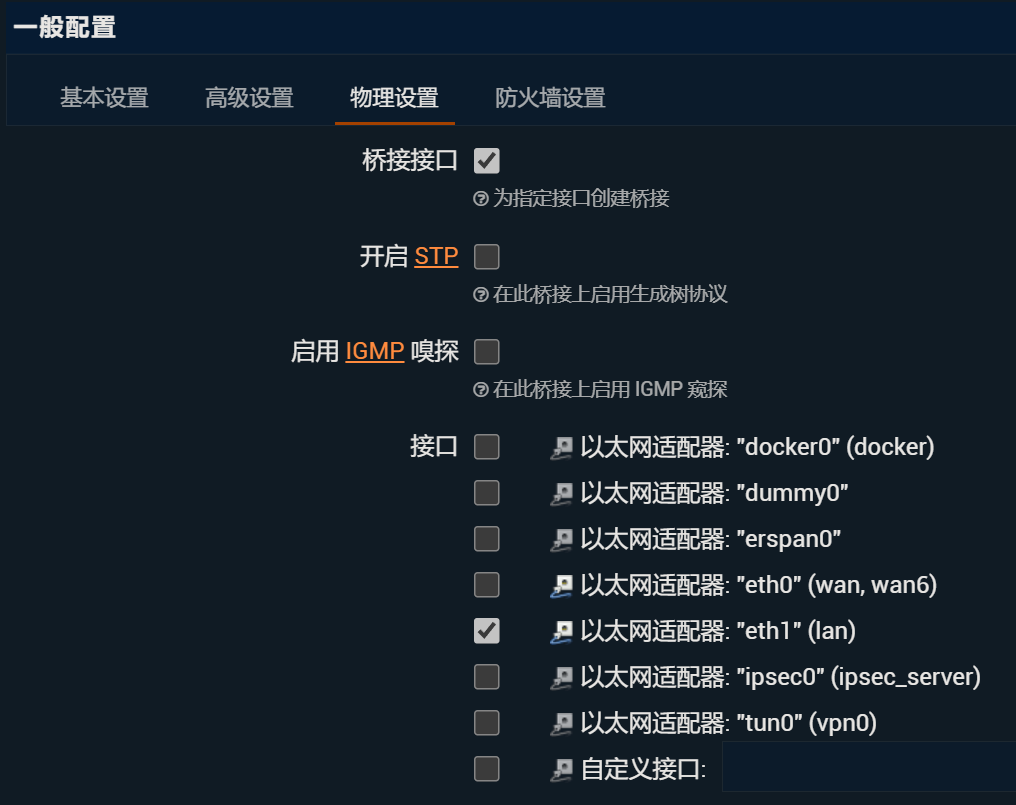
LAN口页面下面的DHCP服务配置:
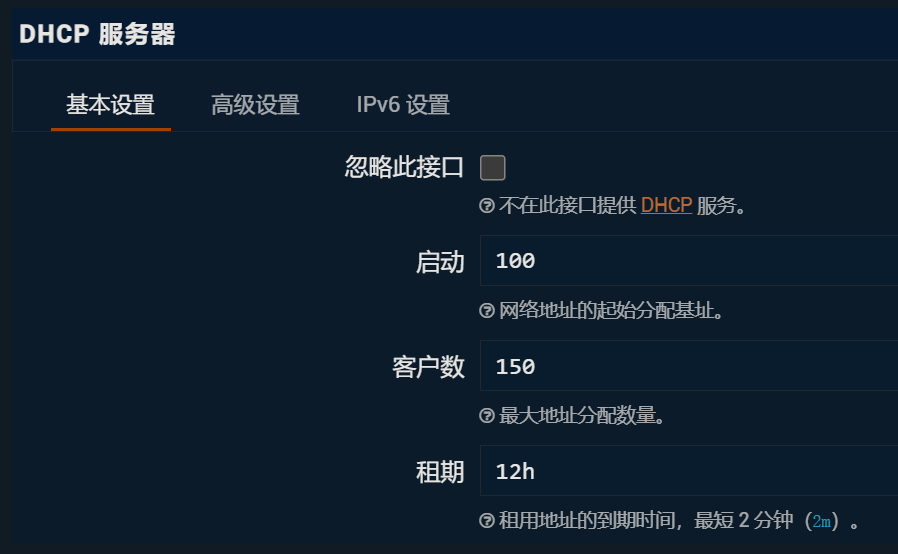
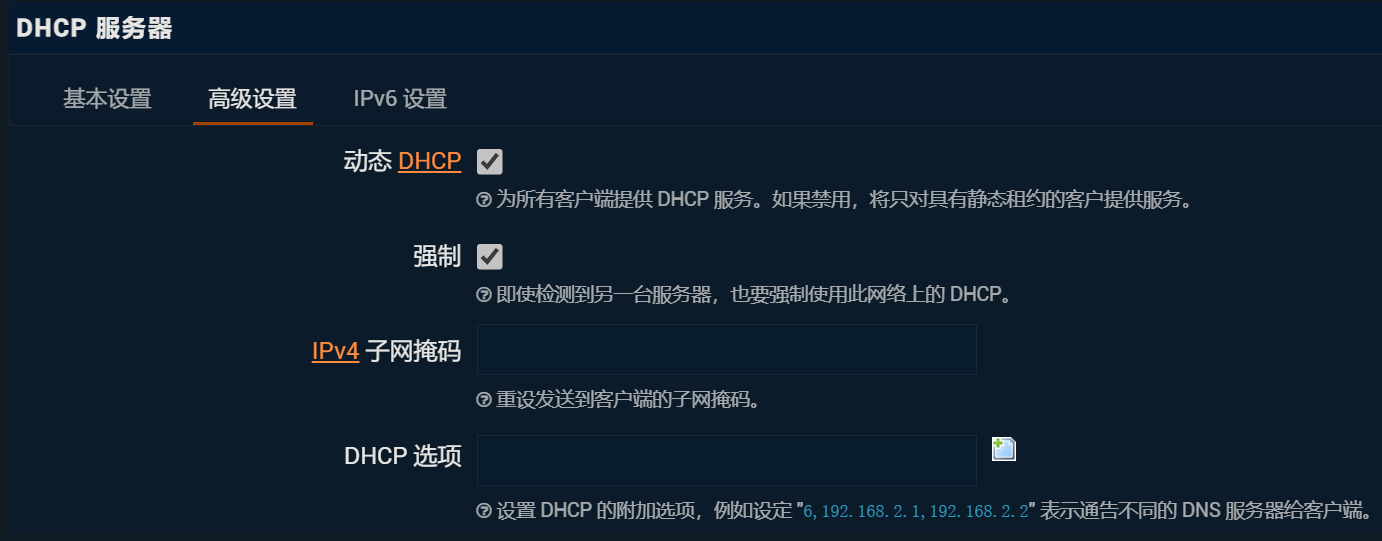

网络-DHCP/DNS配置
重点注意:由于校园网环境需要先在lgn网关进行用户登录,比如在一个172开头的内网进行,而要用的是lgn.bjut.edu.cn来访问,需要用到自动获取的校园网DNS来解析。
在DHCP/DNS配置页面中(服务器设置-基本设置),有一项“重绑定保护”需要取消勾选!不然无法使用内网的DNS,无法访问内网地址。
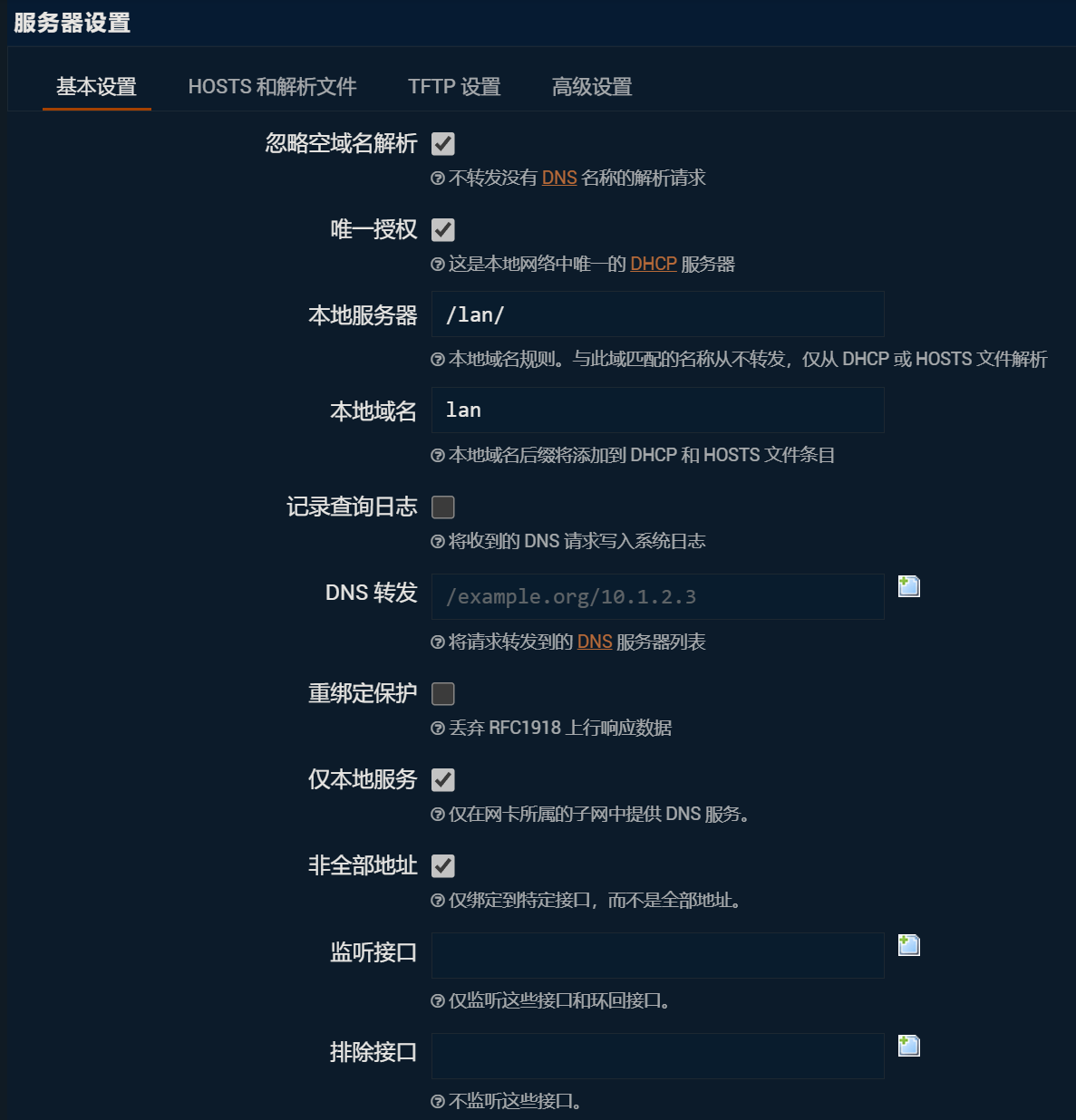
还有一项,如果要使用IPV6环境,务必把高级设置中的“禁止解析 IPV6 DNS 记录”取消勾选。否则无法访问IPV6网址(如lgn6.bjut.edu.cn)。
其他默认即可。

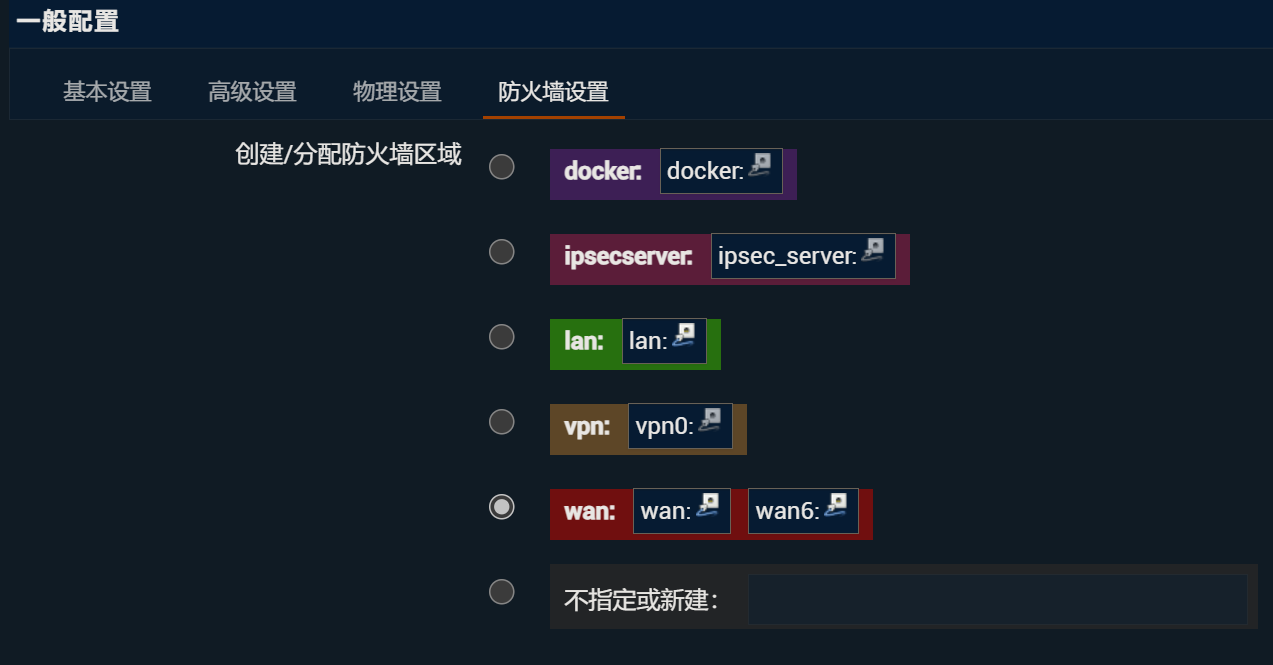
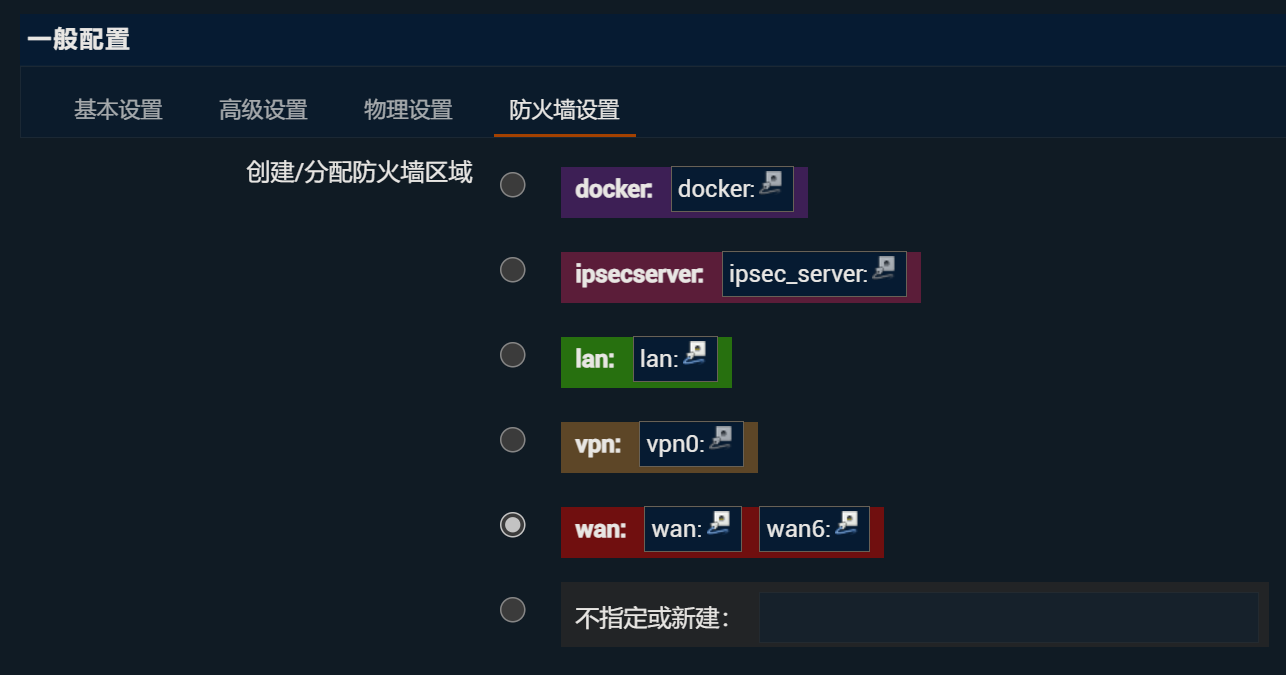
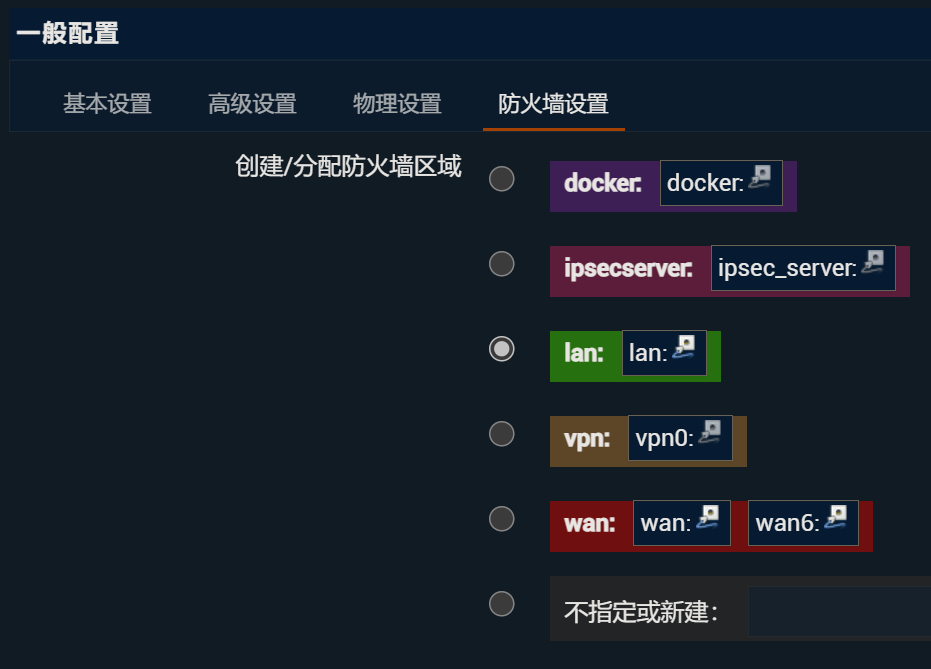
网络-防火墙配置
目前不确定校园网环境下使用OpenWrt时防火墙的默认配置是否有影响。
默认下是这样的:
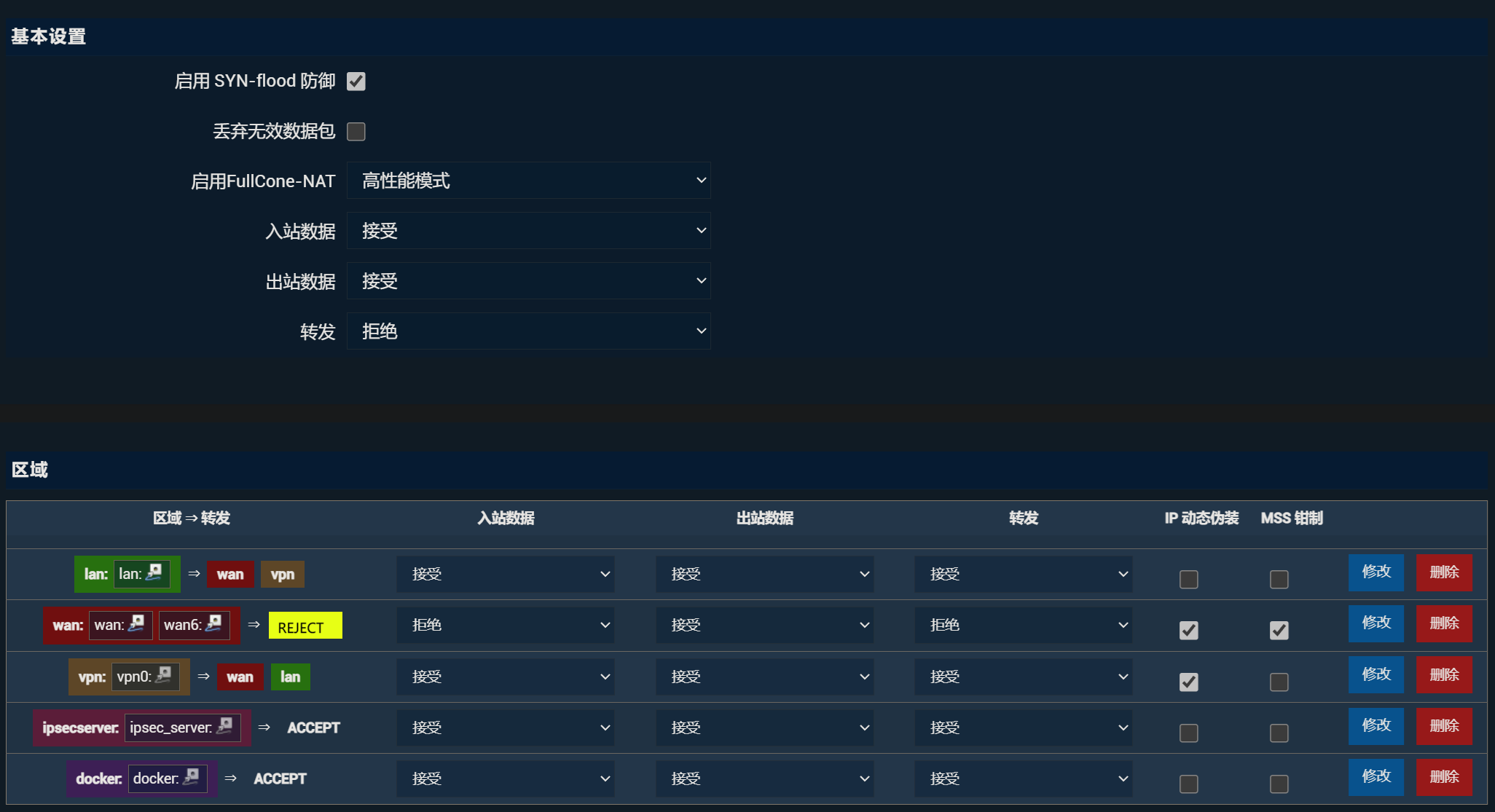
修改后是这样的,即把基本设置的“转发”改为接受。wan口的“入站”、“转发”也改为接受。
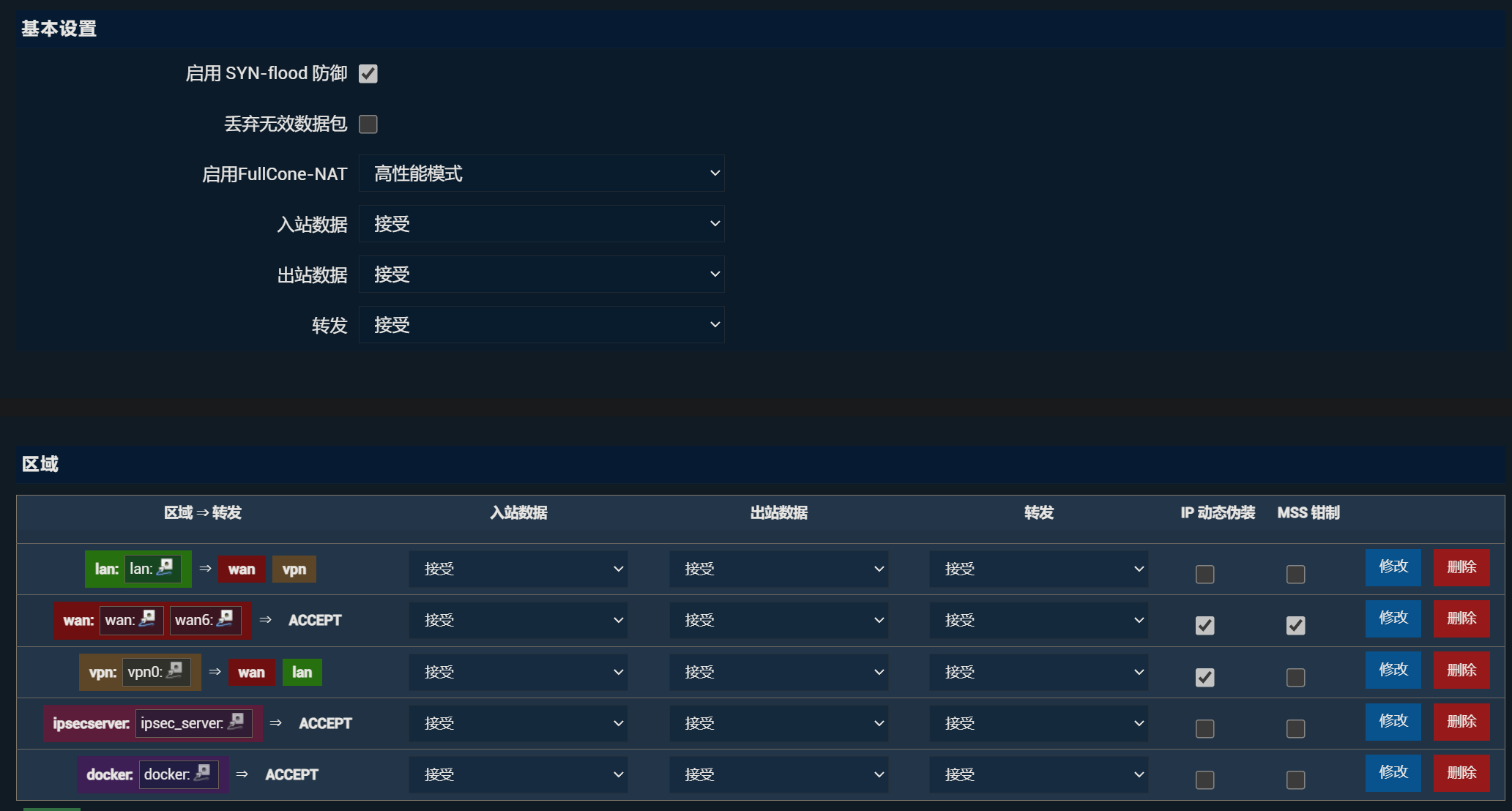
除了基本设置以外,其他的都默认。
AP路由器配置
在开启有线中继时,总是会出现莫名其妙的Bug。比如只有某一个电脑能正常访问lgn6.bjut.edu.cn以及lgn.bjut.edu.cn,其他电脑则只能访问lgn.bjut.edu.cn。更有一种奇葩的现象是那个能正常访问IPV6的电脑有时会无法访问lgn.bjut.edu.cn?
所以干脆就开启正常的路由器模式吧!实测在BJUT的校园网环境下,不会造成多设备识别。网关后台的在网设备只显示了一条设备记录。

路由器型号:Redmi路由器 AX6000
系统ROM版本:MiWiFi 稳定版 1.0.67
设置
常用设置-上网设置中:
上网设置,默认是DHCP。保持不动。
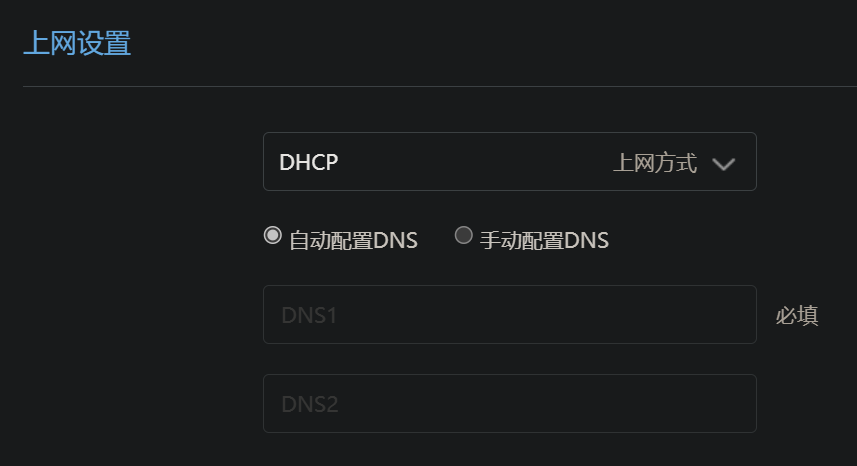
IPV6网络设置,需要打开,修改上网方式为NAT6。
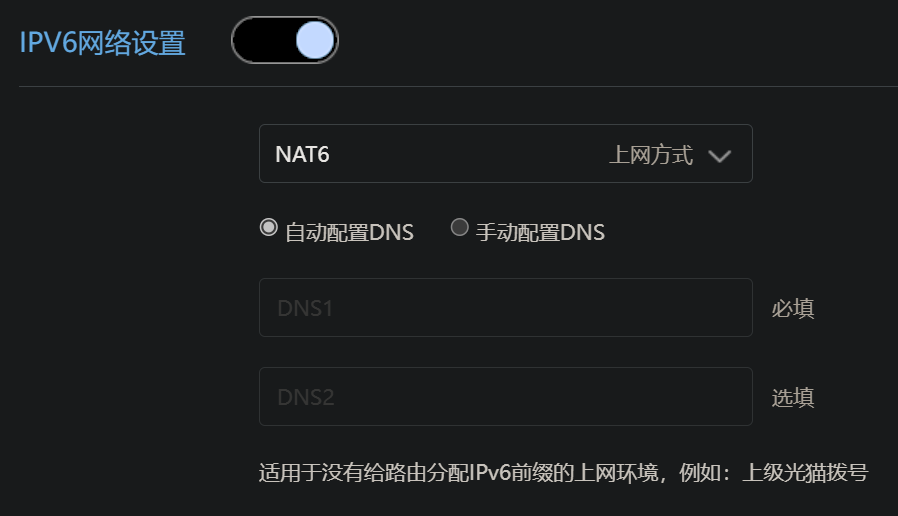
其他保持不变。
正常状态下,上网信息如下显示:
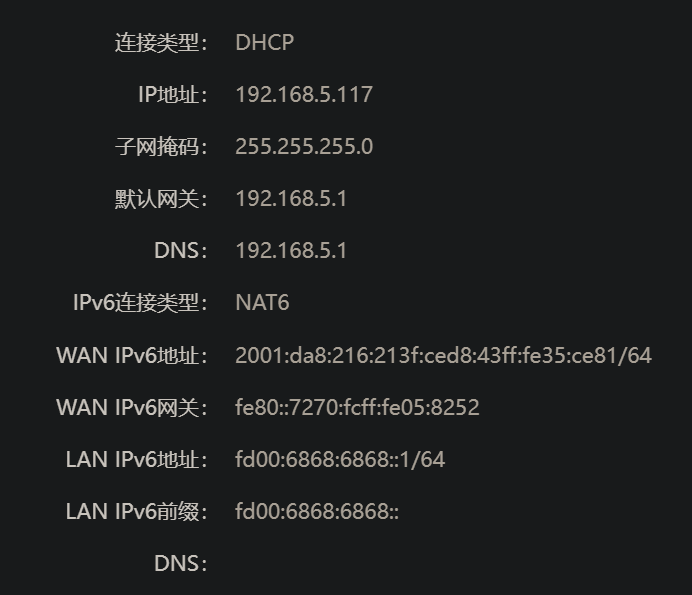
至此,只要一个设备连接了此路由器,在lgn6.bjut.edu.cn进行IPV6、IPV4统一认证后,其他设备直接连接此路由器即可同样地按照统一的方式上网,并且无需再进行认证。
OpenClash配置
通过以上的配置,达到了软路由+AP路由器可以多设备依赖AP路由器的IPV4、IPV6同时上网。
以下,来配置OpenClash,达到丝滑的代理上网效果。
下载内核文件
在“服务-OpenClash”中,进入OpenClash页面。
首先要下载内核。
其自带的下载不好用,网络差时,需要手动下载。
在“插件设置-版本更新”页面,依次点击3个Clash内核对应的“下载到本地”。会从Github上下载3个tar.gz压缩包到你现在的终端机。比如Windows电脑。
我们可以把它解压后,通过OpenWrt中的“系统-文件传输”依次上传到/tmp/upload。
上传后,在Windows终端进行ssh远程连接OpenWrt。
1 | ssh root@192.168.5.1 |
如果弹出了私钥相关的信息,初次访问的话,打一个yes即可。
(也可以在“系统-TTYD 终端”操控OpenWrt终端)
进入终端后,把刚才上传的文件移动到3个内核分别对应的位置。
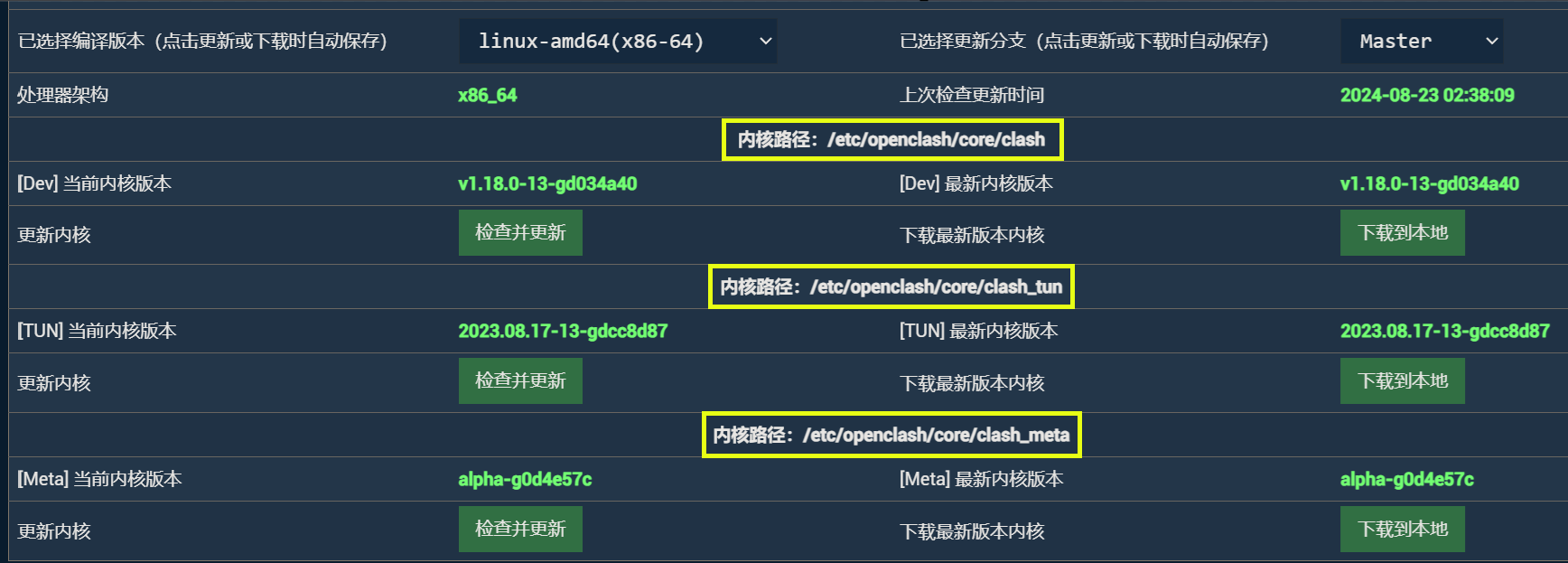
1 | mv /tmp/upload/clash /etc/openclash/core/clash |
移动完后,发现OpenClash不能识别、执行此文件,需要改变权限。
1 | chmod 777 clash |
配置订阅
系统-OpenClash-配置订阅
添加。配置文件名写一个好辨识的,订阅地址按实际的写。一般Clash能用的,都可以。
填完后,保存配置。
上面的自动更新,勾选,更新模式选择“循环”,间隔1440分钟。
填完后,保存配置。最后点更新配置。
配置上网模式
Fake-IP在某些限制比较强的网站(如ChatGPT),可能表现得更好。
点页面下面的“切换页面到Fake-IP模式”。
Meta内核相比其他内核比较活跃,并且支持更多的特性。在模式设置中,勾选“使用Meta内核”。
运行模式,选择Fake-IP(TUN)模式。(因为据说TUN访问网页的响应速度更快)
网络栈类型,下面的小字说“请自行根据运行速度为 TUN 模式选择合适的网络栈”,当前软路由主机的芯片配置还算可以,x86体系的,因此可以选择"Mixed"先试试。
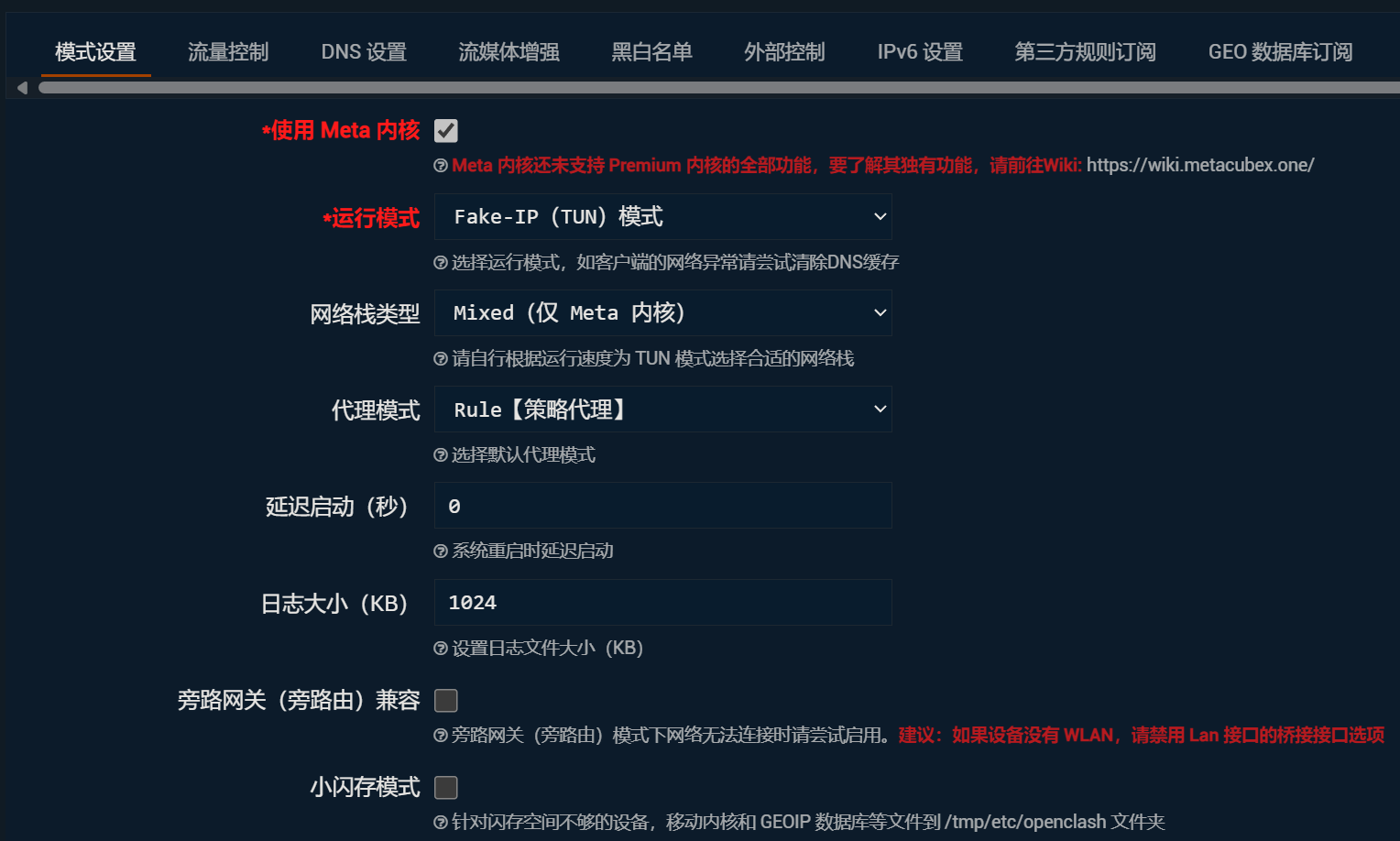
模式设置改完了。先点下面的保存配置,别太快地点应用配置。
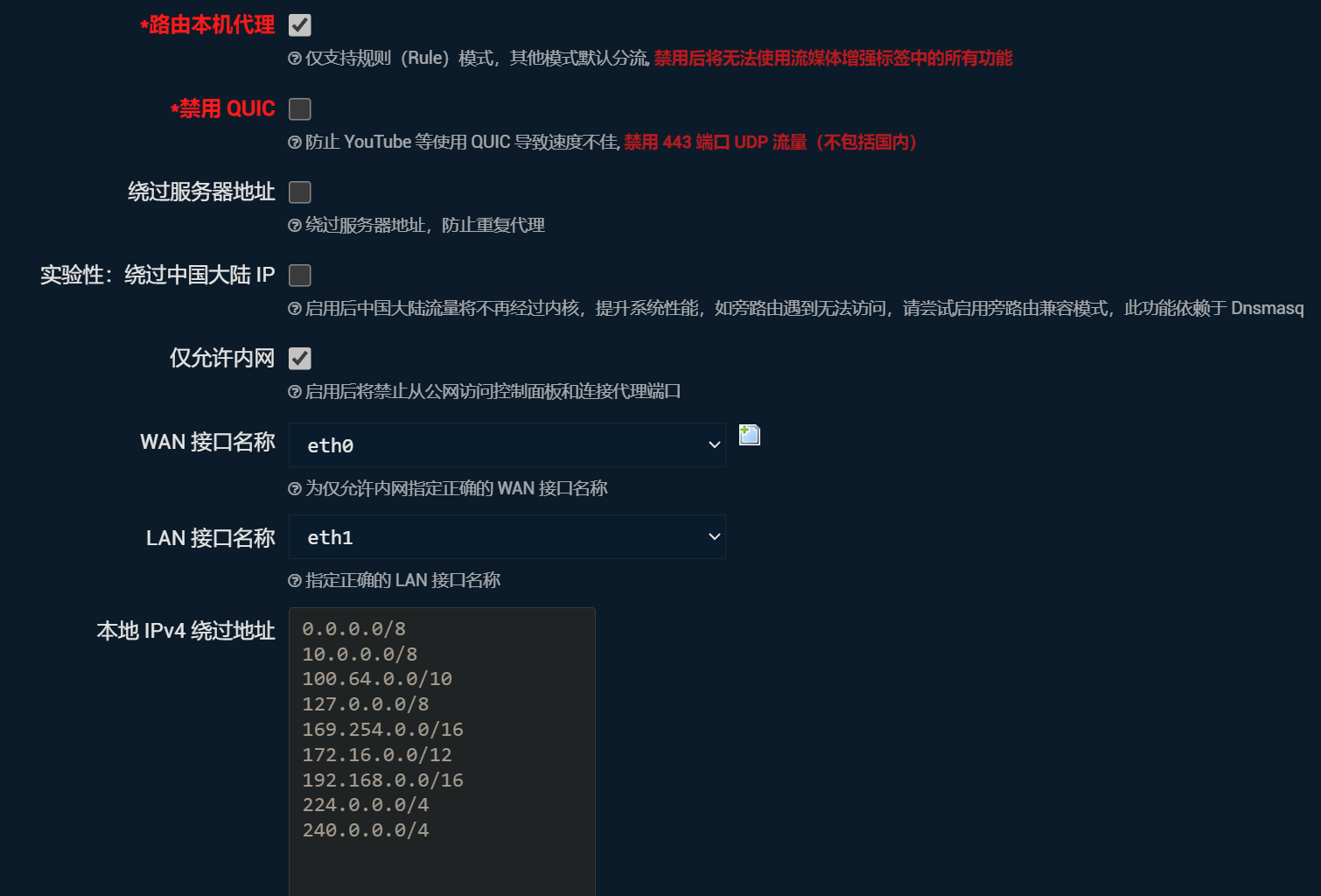
流量控制
取消勾选“禁用QUIC”,因为实测勾选此选项时无法访问Mac端的ChatGPT App。
WAN接口名称、LAN接口名称应正确选择,目前系统的WAN接口是eth0,LAN接口是eth1。
至于“绕过服务器地址”、“绕过大陆IP”,为了避免配置过于复杂,先不勾选。
其他的默认不动。点击保存配置。
DNS设置
由于在校园网环境下使用,需要配置内网DNS。
在DNS设置页面中,勾选“启用第二DNS服务器”,指定服务器为172.21.201.21。(BJUT的DNS有两个,172.21.201.21和172.21.201.20)
下面的域名列表填入一行:*.bjut.edu.cn。
点击保存配置。
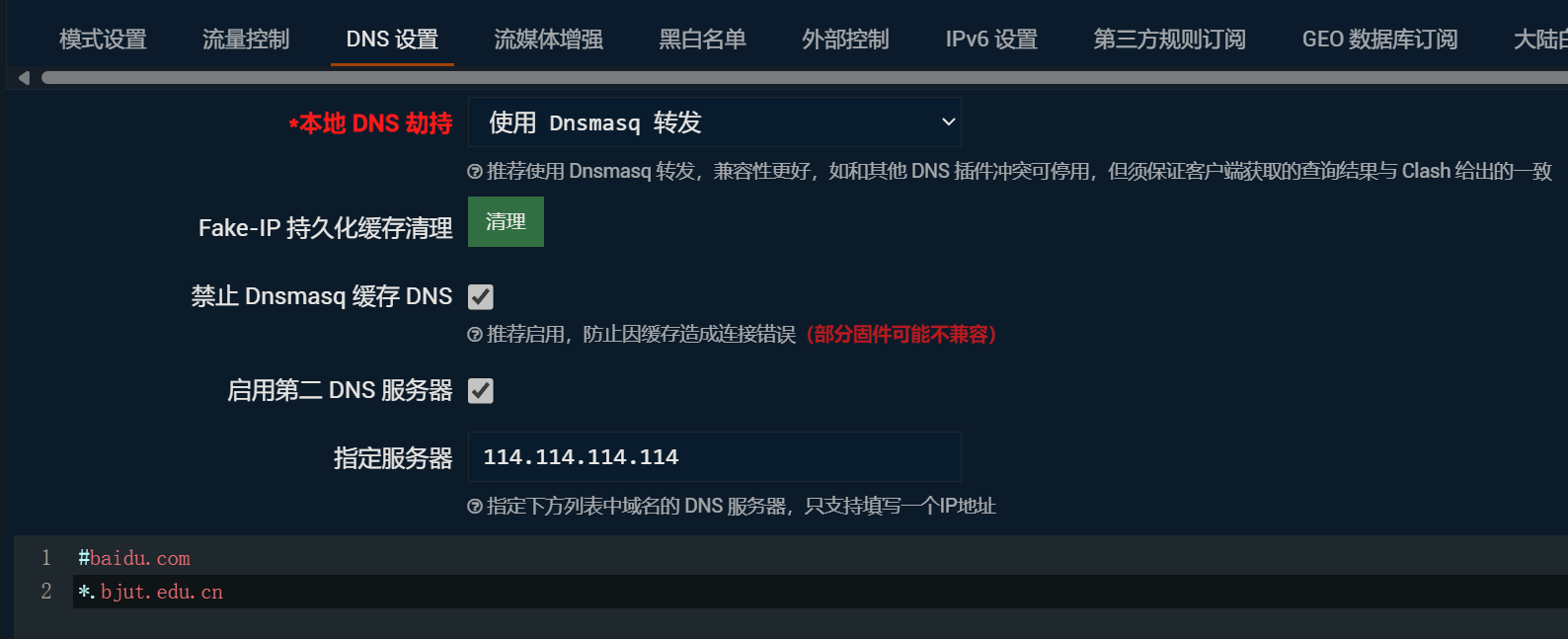
OpenClash推荐使用Dnsmasq转发,但是易用性实在难以恭维,在校园网环境下,先这样凑合用吧!
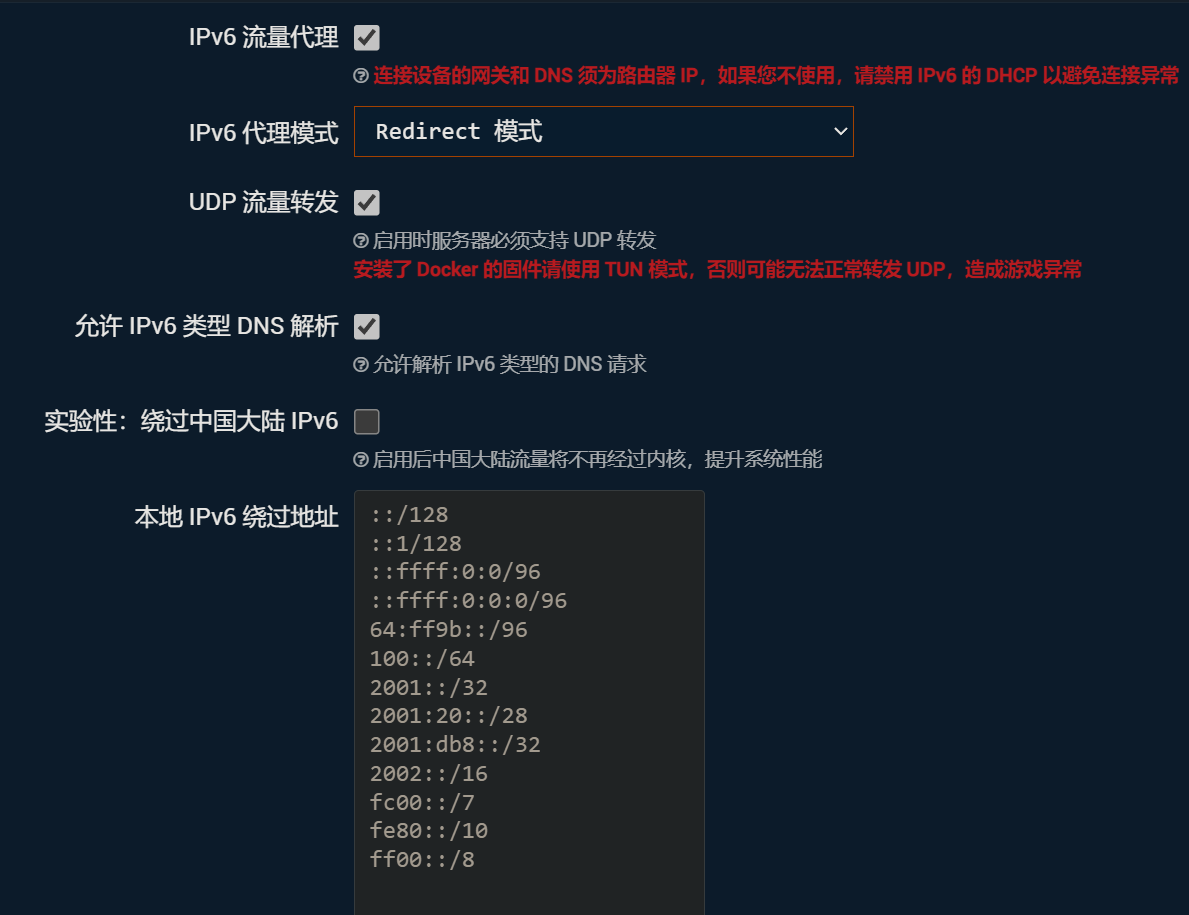
IPV6设置
为了可以在代理上网的同时支持IPV6,需要勾选“IPv6流量代理”、“允许IPv6类型DNS解析”。
除此之外,为了支持更多网站,勾选“UDP流量转发”。
IPv6代理模式选择“Redirect模式”,具体原因忘记了。
其他默认不变,保存配置。
最后
别忘了点应用配置,看看启动效果、上网效果。
可以进3种控制面板选择节点。
再次DNS配置
不幸的是,根据测试,即使启用了第二DNS,也无法正常访问内网,比如lgn.bjut.edu.cn、my.bjut.edu.cn。而如果输入IP地址却能访问,显然还是DNS的问题。
那么只能停用“插件设置-DNS设置”中的“本地DNS劫持”了。
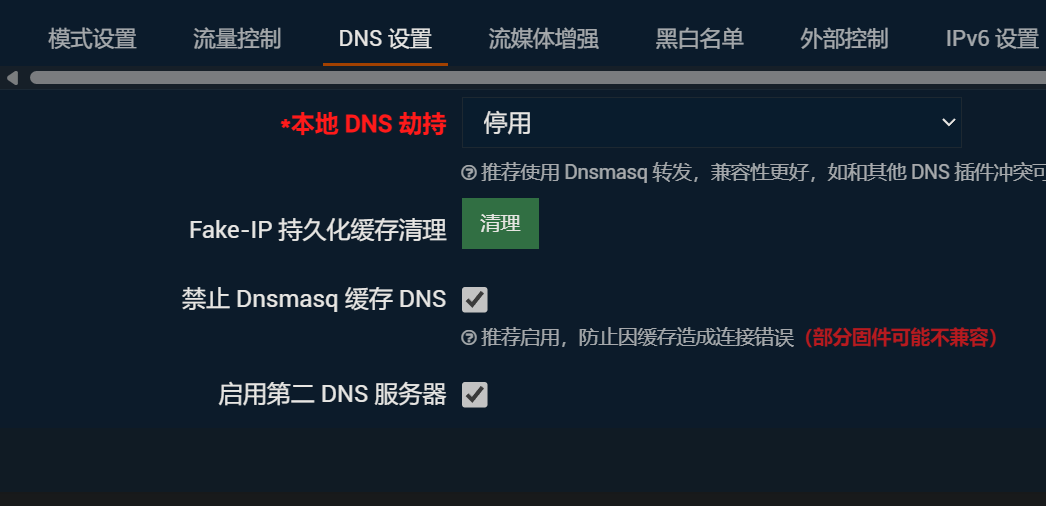
之后,在“覆写设置-DNS设置”中
勾选“自定义上游DNS服务器”、“追加上游DNS”。
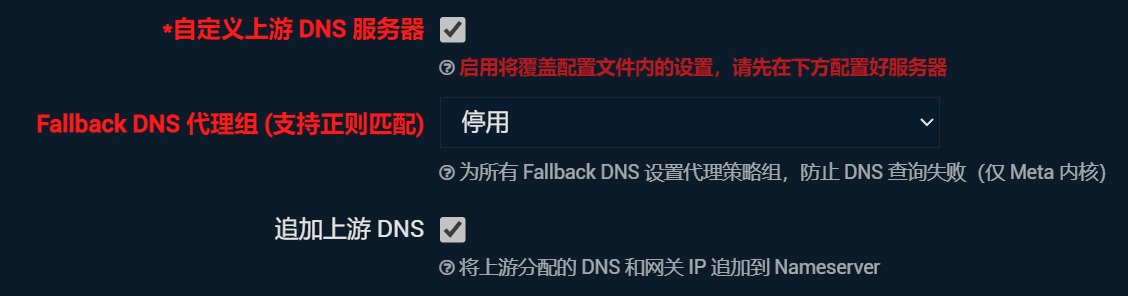
并在下面“设置自定义上游 DNS 服务器”添加一个自定义DNS。
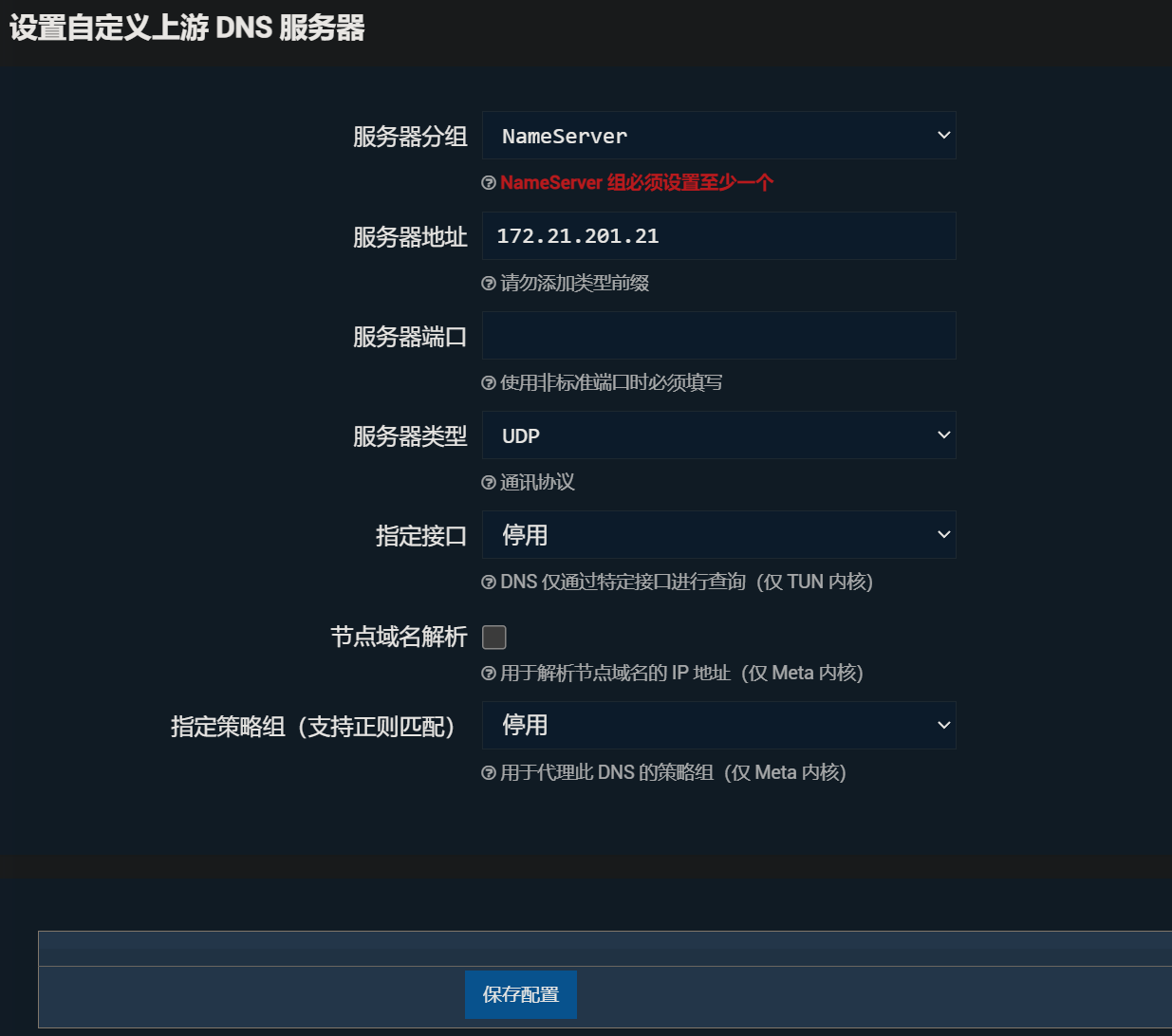

至此,保存配置、应用配置。
就可以访问内网了。
成果
可以多设备连接AP路由器愉快地网上冲浪了!
并且实测,按以上配置,可以不关闭OpenClash的情况下,直接搭配“下载CDN重定向IPV6工具包”正常使用!