CAS_原子操作

发表于2022-05-26更新于2024-07-19阅读次数

内容

  1. CAS原理
  2. 原子操作
  3. 栈
  4. 汇编层面

CAS

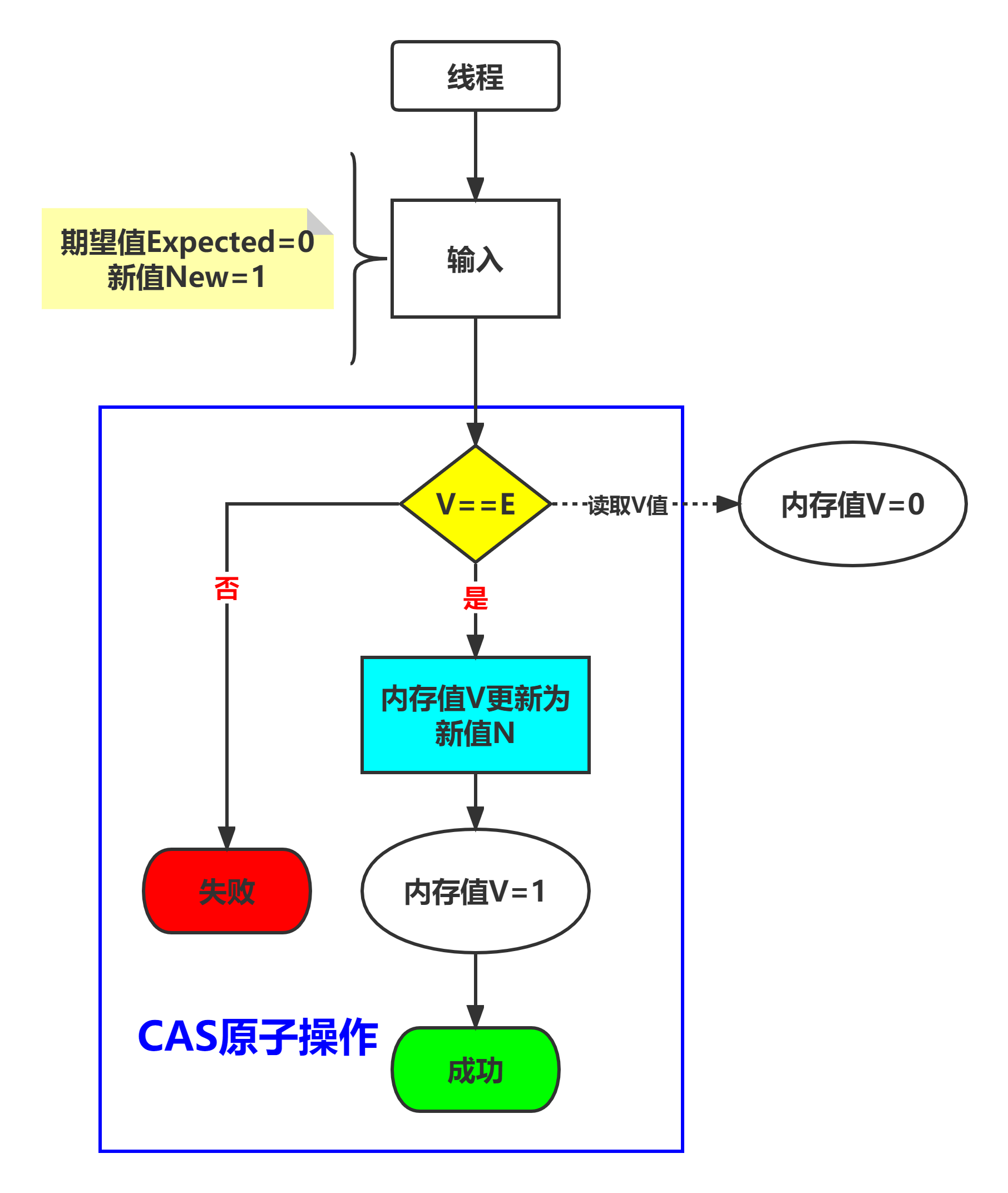
CAS(compare And Swap)也叫比较交换，是一种无锁原子算法，映射到操作系统就是一条cmpxchg硬件汇编指令(保证原子性)，其作用是让CPU将内存值更新为新值，但是有个条件，内存值必须与期望值相同，并且CAS操作无需用户态与内核态切换，直接在用户态对内存进行读写操作(意味着不会阻塞/线程上下文切换)。

它包含3个参数CAS(V，E，N) ，V表示待更新的内存值，E表示预期值，N表示新值，当V值等于E值时，才会将V值更新成N值，如果V值和E值不等，不做更新，这就是一次CAS的操作。

image-20220527162619434

链栈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
#include<mutex>
#include<thread>
template<class T>
class Stack
{
private:
struct StackNode
{
	T data;
	StackNode* next;
};
StackNode* Buynode()
{
	StackNode* s = (StackNode*)malloc(sizeof(StackNode));
	if (NULL == s)exit(1);
	memset(s, 0, sizeof(StackNode));
	return s;
}
void Freenode(StackNode* pnode)
{
	free(pnode);
}
private:
	StackNode* base;
	size_t cursize;
	//mutable std::mutex mtx;
	mutable std::recursive_mutex mtx;
	Stack(const Stack&) = delete;
	Stack& operator=(const Stack&) = delete;
public:
	Stack()
		:base(nullptr), cursize(0)
	{

	}
	~Stack()
	{
		clear();
	}
	void clear()
	{
		std::lock_guard<std::recursive_mutex> locker(mtx);
		while (base != nullptr)
		{
			StackNode* q = base;
			base = q->next;
			(&(q->data))->~T();
			Freenode(q);
			cursize -= 1;
		}
	}
	void push(const T& x)
	{
		std::lock_guard<std::recursive_mutex> locker(mtx);
		StackNode* s = Buynode();
		new(&(s->data)) T(x);	//定位new构造对象
		s->next = base;
		base = s;
		cursize += 1;
	}
	const T& top() const
	{
		std::lock_guard<std::recursive_mutex> locker(mtx);
		return base->data;
	}
	T& top()
	{
		std::lock_guard<std::recursive_mutex> locker(mtx);
		return base->data;
	}
	void pop()
	{
		std::lock_guard<std::recursive_mutex> locker(mtx);
		if (base != nullptr)
		{
			StackNode* q = base;
			base = q->next;
			(&(q->data))->~T();	//定位析构
			Freenode(q);
			cursize -= 1;
		}
	}
public:
	size_t get_size() const
	{
		std::lock_guard<std::recursive_mutex> locker(mtx);
		return cursize;
	}
	bool is_empty() const
	{
		std::lock_guard<std::recursive_mutex> locker(mtx);
		return get_size() == 0;
	}
};
#define _TEST1
#ifdef _TEST1
#include<iostream>
#include<thread>
void thread_funa(Stack<int>& s)
{
	for (int i = 1; i <= 10; i += 2)
	{
		std::cout << i << std::endl;
		s.push(i);
	}
}
void thread_funb(Stack<int>& s)
{
	for (int i = 2; i <= 10; i += 2)
	{
		std::cout << i << std::endl;
		s.push(i);
	}
}
int main()
{
	Stack<int> ist;
	std::thread tha(thread_funa, std::ref(ist));
	std::thread thb(thread_funb, std::ref(ist));

	tha.join();
	thb.join();
	std::cout << "push over." << std::endl;
	while (!ist.is_empty())
	{
		int val = ist.top();
		std::cout << val << std::endl;
		ist.pop();
	}
}
#endif

结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
12

43

65

87

109

push over.
9
10
7
8
5
6
3
4
1
2

标准库原子操作API

构造函数

原型：std::atomic<T>::atomic

1
2
3
4
atomic() noexcept = default;
constexpr atomic() = noexcept(std::is_nothrow_default_constructible_v<T>);
constexpr atomic(T desired) noexcept;
atomic(const atomic&) = delete;

有默认无参构造；拷贝构造删除。

operator=

1
2
3
4
T operator=(T desired) noexcept;
T operator=(T desired) volatile noexcept;
atomic& operator=(const atomic&) = delete;
atomic& operator=(const atomic&) volatile = delete;

两个原子对象之间不可相互赋值。

代码示例

1
2
3
4
5
6
7
8
#include<atomic>
int main()
{
    atomic<int> iat;
    atomic<int> iat2;
    //iat = iat2; //error
    iat = 10;
}

load

原子地加载并返回原子对象的当前值。安装order的值影响内存。

1
2
3
4
5
6
T load(std::memory_order order = std::memory_order_seq_cst) const noexcept;
T load(std::memory_order order = std::memory_order_seq_cst) const volatile noexcept;
参数：
    order	- 强制的内存顺数
返回值：
    原子变量的当前值
1
2
3
4
5
6
7
8
#include<atomic>
int main()
{
    atomic<int> iat;
    atomic<int> iat2;
    iat = 10;
    int val = iat.load();
}

存在的问题：

语义是获取原子对象的值没错，但是获取的此值只作为当时的瞬时值。

在多线程中，可能获得的是脏数据。

compare_exchange

有两个函数。compare_exchange_weak、compare_exchange_strong。

原子地比较原子对象与的非原子参数的值，若相等进行交换，若不相等则进行加载。

1
2
3
4
5
6
7
8
9
bool compare_exchange_weak(T & expected, T desired, std::memory_order order = std::memory_order_seq_cst) noexcept;
参数：
	expected - 到期待在原子对象中找到的值的引用。若比较失败则被存储*this的实际值。
	desired  - 若符合期待则存储于原子对象的值
	success  - 若比较成功,则读修改写操作所用的内存同步顺序。容许所有值。
	failure  - 若比较失败,则加载操作所用的内存同步顺序。不能为std::memory_order_release或std::memory_order_acq_rel，且不能指定强于success 的顺序(C++17前)
    order 	 - 两个操作所用的内存同步顺序
返回值：
	若成功更改底层原子值则为true，否则为false

原子地比较*this原子对象与expected的对象表示(C++20前) | 值表示(C++20起)，而若它们逐位相等则以desired替换前者（进行读修改写操作）。否则，将*this中的实际值加载进expected（进行加载操作）。

读修改写和加载操作的内存模型分别为success和failure。在上面这个函数中，order用于读修改写操作和加载操作，除了若order == std::memory_order_acq_rel或order== std::memory_order_release，则加载操作分别使用std::memory_order_acquire和std::memory_order_relaxed。

改写链栈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include<mutex>
#include<thread>
template<class T>
class Stack
{
private:
struct StackNode
{
	T data;
	StackNode* next;
};
StackNode* Buynode()
{
	StackNode* s = (StackNode*)malloc(sizeof(StackNode));
	if (NULL == s)exit(1);
	memset(s, 0, sizeof(StackNode));
	return s;
}
void Freenode(StackNode* pnode)
{
	free(pnode);
}
private:
	mutable std::atomic<StackNode*> pHead;
	Stack(const Stack&) = delete;
	Stack& operator=(const Stack&) = delete;
public:
	Stack()
		:pHead(nullptr)
	{

	}
	~Stack()
	{
		
	}
    void push(const T& val)
    {
        StackNode * newnode = Buynode();
        new(&(newnode->data)) T(val);
        newnode->next = pHead;
        pHead = newnode;
    }
};
int main()
{
    Stack<int> ist;
    
}

对newnode->next = pHead; pHead = newnode;进行原子化。
即转为：while(!pHead.compare_exchange_weak(newnode->next, newnode));

1
2
3
4
5
6
7
8
void push(const T& val)
{
    StackNode * newnode = Buynode();
    new(&(newnode->data)) T(val);
    
    newnode->next = pHead.load();
    while(!pHead.compare_exchange_weak(newnode->next, newnode));
}

判断pHead是否等于newnode->next，如果相等，则把newnode赋值给pHead。

Linux线程调度策略

发表于2022-05-26更新于2025-11-04阅读次数

内容

  1. 先来先服务（FIFO）调度策略
  2. 时间片轮转调度策略
  3. 分时调度策略

Linux内核线程的三种调度策略

函数pthread_attr_setschedpolicy和pthread_attr_getschedpolicy分别用来设置、获取线程的调度策略。

1
2
3
4
5
6
7
int pthread_attr_setschedpolicy(pthread_attr_t *, int policy);
int pthread_attr_getschedpolicy(const pthread_attr_t *, int policy);
参数：
    attr 	- 线程属性变量
    policy	- 调度策略
返回值
    成功返回0，失败返回-1
  1. SCHED_OTHER：分时调度策略，非实时。不支持优先级。
  2. SCHED_FIFO：先到先服务，实时。一旦占用cpu则一直运行。直到有更高优先级任务或主动放弃cpu。
  3. SCHED_RR：时间片轮转，实时。当进程的时间片用完，重新分配时间片长度，置于就绪队列尾。可以看作是FIFO的延伸。

先到先服务策略

  1. 创建进程时指定采用FIFO，并设置实时优先级rt_priority(1-99)。
  2. 如果没有等待资源，则将该任务加入到就绪队列中。
  3. 调度程序遍历就绪队列，根据实时优先级计算调度权值(1000+rt_priority)，选择权值最高的任务使用cpu，该FIFO任务将一直占有cpu直到有优先级更高的任务就绪(即使优先级相同也不行)或者主动放弃(等待资源)。
  4. 调度程序发现有优先级更高的任务到达(高优先级任务可能被中断或定时器任务唤醒，再或被当前运行的任务唤醒等等)，则调度程序立即在当前任务堆栈中保存当前cpu寄存器的所有数据，重新从高优先级任务的堆栈中加载寄存器数据到cpu，此时高优先级的任务开始运行。重复第3步。
  5. 如果当前任务因等待资源而主动放弃cpu使用权，则该任务将从就绪队列中删除，加入等待队列，此时重复第3步。

时间片轮转策略

所有任务都采用RR调度策略时：

  1. 创建任务时指定调度参数为RR，并设置任务的实时优先级和nice值(nice值将会转换为该任务的时间片的长度)。

    可见，相比于FIFO，时间片轮转法多了一个nice值，用于计算时间片长度。

  2. 如果没有等待资源，则将该任务加入到就绪队列中。

  3. 调度程序遍历就绪队列，根据实时优先级计算调度权值(1000+rt_priority)，选择权值最高的任务使用cpu。

    相比于FIFO，FIFO会一直占用CPU，直到更高优先级线程到达。

  4. 如果就绪队列中的RR任务时间片为0，则会根据nice值设置该任务的时间片，同时将该任务放入就绪队列的末尾。重复步骤3。

  5. 当前任务由于等待资源而主动退出cpu，则其加入等待队列中。重复步骤3。

分时调度策略

所有任务都采用Linux分时调度策略时：

  1. 创建任务指定采用分时调度策略，并指定nice值(-20~19, 可以认为值越小优先级越高)。

    相比于FIFO，没有实时优先级数值属性(1~99)

  2. 将根据每个任务的nice值确定在cpu上的执行时间(counter)。

  3. 如果没有等待资源，则将该任务加入到就绪队列中。

  4. 调度程序遍历就绪队列中的任务，通过对每个任务动态优先级的计算权值(counter+20-nice)结果，选择计算结果最大的一个去运行，当这个时间片用完后(counter减至0)或者主动放弃cpu时，该任务将被放在就绪队列末尾(时间片用完)或等待队列(因等待资源而放弃cpu)中。

  5. 此时调度程序重复上面计算过程，转到第4步。

  6. 当调度程序发现所有就绪任务计算所得的权值都不大于0时，重复第2步。

区别

系统中既有分时调度，又有时间片轮转调度和先进先出调度：

  1. RR调度和FIFO调度的进程属于实时进程，以分时调度的进程是非实时进程。
  2. 当实时进程准备就绪后，如果当前cpu正在运行非实时进程，则实时进程立即抢占非实时进程。
  3. RR进程和FIFO进程都采用实时优先级做为调度的权值标准，RR是FIFO的一个延伸。
  4. FIFO时，如果两个进程的优先级一样，则这两个优先级一样的进程具体执行哪一个是由其在队列中的未知决定的，这样导致一些不公正性（优先级是一样的，为什么要让你一直运行？），如果将两个优先级一样的任务的调度策略都设为RR，则保证了这两个任务可以循环执行，保证了公平。